9.実験計画法
はじめに
実験計画法は、どのように実験すればよいかを数学的に解決する方法です。
しかし、QC検定2級ではそこまでの知識は必要なく実験の結果をどう解釈するかのみとなっています。
実験は何が有用(効果)があるのか調べるのが目的ですが実験すると、どうしても誤差も発生します。
誤差を上手に取り扱うことができたら効果がより分かりやすくなり判断が容易になるはずです。
誤差の取り扱いには
- 実験値を効果と誤差に分離する
- 分離できたならば、実験の効果はいくらなのか
- 2で得た効果は誤差によってあるようにみえていないか確認
があり、それをこの項では説明していきます。
でも、その解説の前に統計学独特の用語を説明します。
用語
第八章の相関で勉強したように加熱時間によって強度が変化するものがあったとします。
この時、強度のように実験の結果表れる製品の品質を『特性』と言います。
そして加熱時間によって強度が変化したならば もしかしたら加熱温度によっても強度が変化するかもしれません。
このように、特性に影響を与えそうな要素を『要因』 といいます。
しかし、要因には加熱時間・加熱温度以外にも加熱後の冷却時間・冷却温度などもあるかもしれません。
しかしそれら全てを実験するのは不可能で特に実験に取り上げる要因を『因子』と言います。
相関では、加熱温度を20、30、40、50、60と変化させて測定しました。
このように実験を行うにあたって因子の値を様々に変えますが、実験における因子の 条件を『水準』と言います。
そして相関のような実験の場合、水準数が4つあり、最も良い水準は50であると言います。
(水準60は実験していないので 今回のはなしにはあてはまらない)
最後に、今回の場合 取り扱ったのは加熱時間だけですが、取り上げた因子のもたらす影響を『主効果』 と言い、加熱時間と加熱温度のように複数の因子を組み合わせて発生する効果を『交互作用』 と言います。
①実験値を効果と誤差に分離する
それでは、実際に数学的にどのように実験値を効果と誤差に分離するか見てみましょう。
とはいっても誤差を除去するには残念ながら同じ状態での実験を数回行う必要があります。
9章の相関で行った実験を3回繰り返し表9.1ができました。
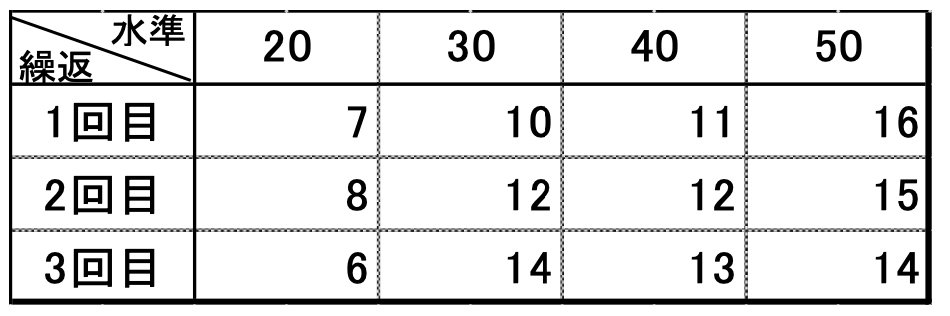
表9.1 (図8.1から抽出したものも含む)
誤差はプラスの方向にもマイナスの方向にも偏りなく発生するはずなので誤差がない値とは同水準で繰り返して得られた値の平均と考えることができます。
そのように考えると、水準20の実験値は7、8、6なのでその平均は(7+8+6)÷3=7となり、これが、誤差がない場合に取る値ではないかと考えられます。
そうすると、水準20 2回目の実験値8という値は、誤差がない値7と誤差1で構成されていると考えられるのです。
そのため平均は、誤差がないならばこうなるだろうと期待されるのため期待値ともいいます。
② 分離できたならば、実験の効果はいくらなのか
それぞれの水準の効果はいくらか?
表9.1の全ての実験値の平均は(7+8+6+10+12…15+14)÷12=11.5となります。
また水準20のみの平均は(7+8+6)÷3=7となります。
先ほどの誤差の分離の考え方と同様、『全ての水準を加味した平均値は各水準の効果が無いと考えた場合の値』と考えることが出来ます。
誤差同様、平均することでそれぞれの効果を打ち消してしていると考えるのです。
そう考えますと、水準の効果が無い場合の平均値11.5が水準20の場合(平均値)は7となっているのですから水準20の効果は7-11.5=-4..5となります。
②・③で得た効果は誤差によってあるようにみえていないか確認
本当に効果があるのか(水準間のばらつきは誤差のばらつきを超えているか) しかし、本当にそうでしょうか?
もしかしたら、誤差のためにたまたま水準間で差があるように見えているだけかもしれません。
そこで、誤差のばらつきより水準間の効果のばらつきが大きいならば、誤差のばらつきだけではその現象は説明できない、つまり水準間の効果があると判断できます。
そのため、この2つの関係を1つの数字で示すには『水準間で生じるばらつき ÷ 誤差で生じるばらつき』 で算出します。
最も良い条件は何か
5項で水準によって効果があると判断したならば、(当然 ない場合もありその場合プーリング などの処理がありますがここでは説明しません)、最も良い水準は何かを考える必要があります。
というのも5項では水準を設けることに意味があったと分かっただけで、その効果が大きいか小さいかは分かっていません。
とはいえその算出は簡単で、ただそれぞれの水準間の平均(期待値)を算出し、値が大きい方が良いならば、最も大きい期待値である水準が良い水準となるだけです。
3から6項でざっと一連の作業を見てきましたが、次ページから全てのデータ値に関して①・②・③をどのようにしているか詳しく説明していきます。
繰返しになりますが、水準間の違いで発生する効果は、それぞれの水準の平均値(期待値) から全平均を差し引けば計算されます。(図9.1 緑枠参照)
次に、誤差によって生じるばらつきは、水準間の効果を認めるのだから、それぞれの値からそれに属する水準の平均値を差し引けば求められるのです。(図9.1 黄枠参照)
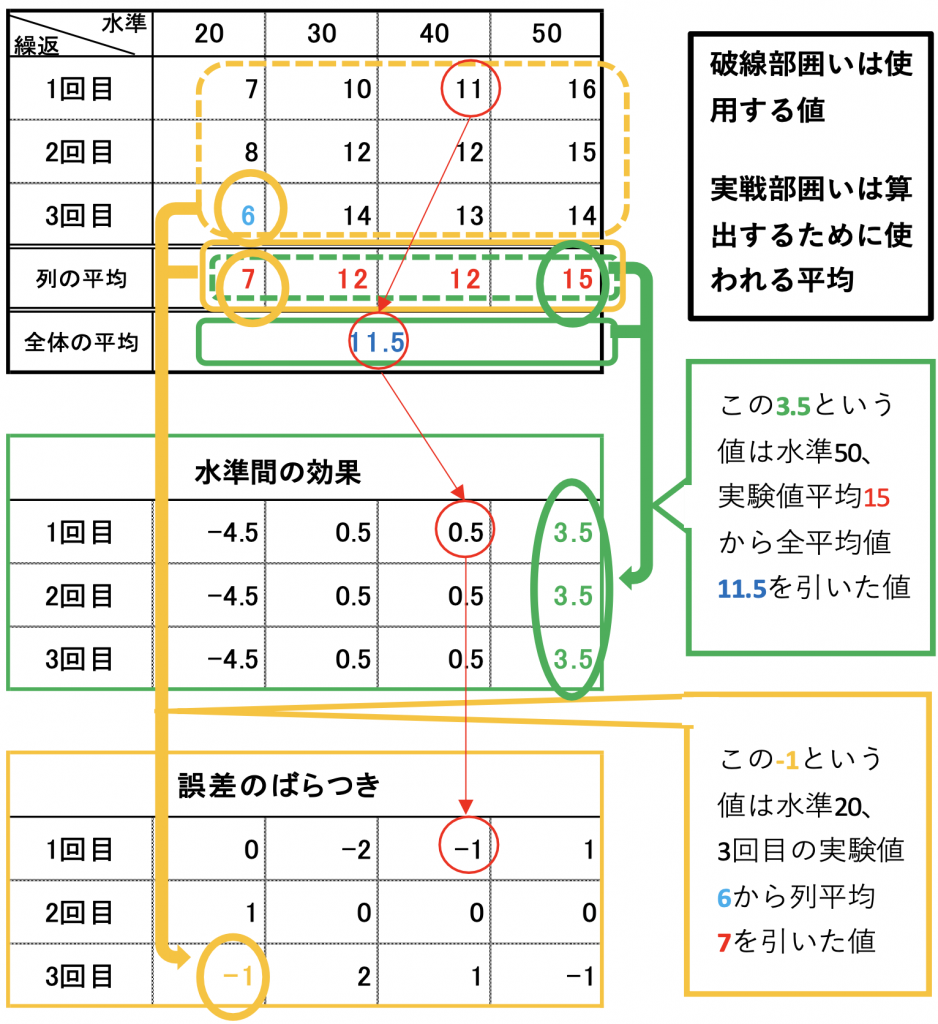
図9.1 データの分解
この表の見方ですが、水準40で1回目の値11を例に見てみます。
(赤丸囲い部が対象です) 実験計画法では、この11という値は水準の効果が無い場合取るであろう値(区間20から50限定ですが) 11.5に水準40での効果 0.5 と誤差 -1 が加わって構成されたと考えているのです。
式で表すと
実験値11 = 水準の効果が無い場合取りうる値11.5 + 水準40の効果 0.5 + 誤差 -1
になります。
ところで、ばらつき(不偏分散)は下記の式で求められました。

ここで分散を自由度と平方和を用いて記入しましたが、実はこの分野では自由度はn-1のように簡単にはならないので、このように記載したのです。
本当に効果があるのか(自由度に関して)
自由度がn-1になる理由を少し記載します。
とはいうものの、この第9章7項は理解しなくても問題 がないので、何度か実験計画法の例題を解いたのちに再度読んでください。
自由度は読んで字のごとし自由になる数のことです。 例えば、平均が6の母集団から標本を3つ取り出した時5、6、8がとれたとします。
この場合、標本の平均は(5+6+8)÷3=6.33で母集団の平均と標本の平均は異なってしまいました。
しかし、標本平均の値と母集団平均の値は同じになるのが理想なのですから、もう一つ標本を取る場合、5の値を取る標本を取るのが理想です。
(5+6+8+5)÷4=6
つまり標本を4つ取る場合、最初の3つまではどんな値の標本を取ってきても良いのですが、最後 の1個は母集団の平均と同じになるような値の標本を取ることが求められるのです。
いいかえれば標本数-1個はどんな値を取っても良い(自由な値を取れる)数であり、これを自由度 と言うのです。
従って自由度とは『ある値を算出する際に、自由に取れる標本数のこと』となります。
そして実験計画法のように 本来ならば同じ値を取るのが理想であるかたまりを扱う (具体的には 表9.1の水準20の場合 7,8,6の値を取ったが これをひとかたまり つまり群と考える)場合 『その対象となる群または値 – 関係のある式(主に平均)の数』 (9.1) で算出されます。
それでは、具体的に(9.1)式を使ってそれぞれの自由度を算出します。
水準間の効果の場合、4つの群つまり7、12、12、15を元にしました。
(図9.1 緑破線囲い部)
そしてそれを全平均11.5つまり1個の平均で差し引き算出したのでした。
算出された値は-4.5 0.5 0.5 3.5です。
結果、自由度は4(群の数) – 1(使った平均値数) = 3 となります。
次に誤差のばらつきの場合、7、8、6、10、12、14、11、12、13、16、15、14と12個の値が元になります。
またこれを4つの平均値7、12、12、15 で差し引き求めたのでした。
算出した値は0、1、-1、-2、0、2、-1、0、1、1、0、-1です。
結果、自由度は12(データ数) – 4(使った平均値数) = 8 自由度は8となります。
本当に効果があるのか(実際の算出)
8項の最後の方でも書きましたが 全ての個々のデータのばらつきは水準間で生じる効果と誤差から構成されています。
言い換えれば全平方和は全水準間平方和と全誤差の平方和ともいえ次式が成り立つのです。
𝑠𝑇 = 𝑠𝐴 + 𝑠𝐸
𝑠𝑇:全ての平方和
𝑠𝐴:𝐴水準の平方和
𝑠𝐸:𝐴誤差の平方和
(9.2)
この関係は自由度にも当てはめることができ

(9.3) の関係があります。
このことを図示すると図9.2のようになります。(図9.1と図9.2は同じもの)
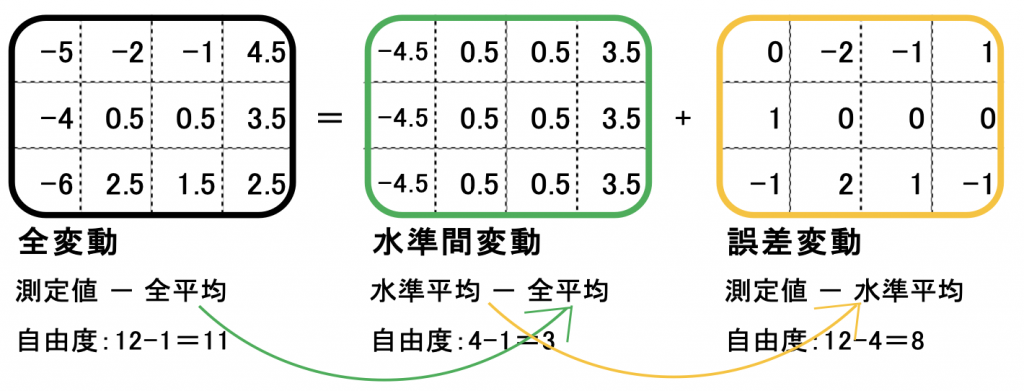
図9.2
それでは関係が分かったところで、水準間の平方和を求めます。
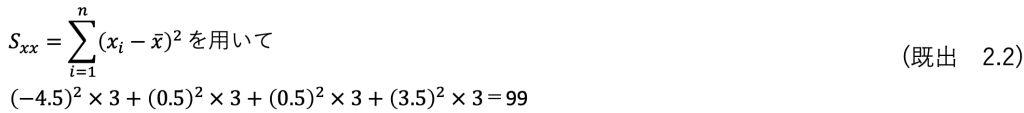
で計算してもよいのですが、せっかく簡単に平方和が計算できる式

を勉強したので、これを使います。
また、今回扱う分散は2つ(水準間の効果と誤差)でした。
そのため
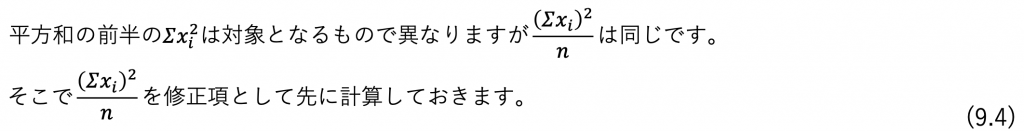
そして、下記に示す修正項や総平方和などの計算を比較的簡単にするために表9.2を作成します。
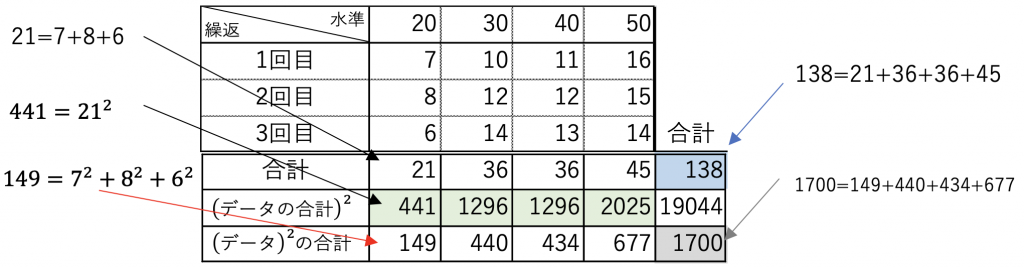
表9.2

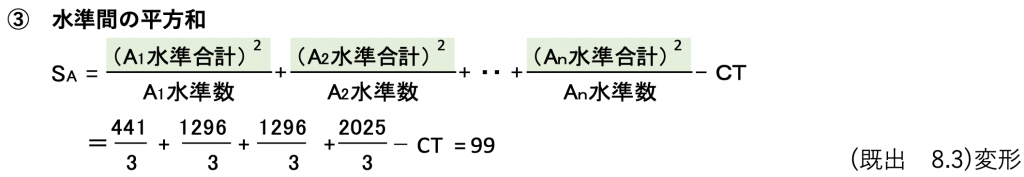
なぜ3で割るかというとA1水準は3個のデータが集まってできており、そのままだと3個の効果になってしまいます。
2で求めたSTは1個当たりの効果ですので、単位を揃えるために構成しているデータ数3で除算するのです。

以上をまとめて一覧表にすると表9.3(公式)⇒ 表9.4(実際の値)のような分散分析表が出来ます。
表9.3の実際の計算は図9.3の関係に示すように最初にSTを記載後SAを記載。
最後にSEをST-SAで計算し記載。
その後、各自由度を算出し不偏分散は平方和÷自由度で算出 F値はVA÷VEで算出し表を埋めます。
表の順序とは異なる順で埋めるようになることになりますが仕方ないです。
また表9.3の自由度は 第9章7項及び式9.3を参照にしてください。

表9.3の式に従って計算した結果は表9.4のようになります。
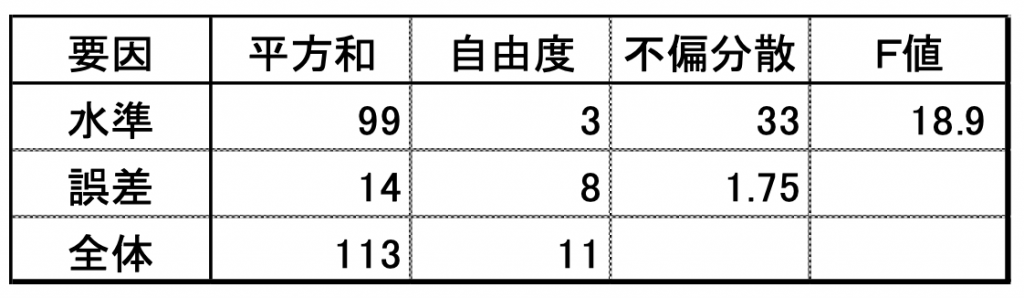
表9.4
となります。
そして、帰無仮説を各水準の母平均がすべて等しい、対立仮説は少なくとも1つの水準において母平均が他と異なるとし片側検定で
- F0 < F(φA 、φE 、;α)ならば有意差なし
- F0 > F(φA 、φE 、;α)ならば有意差あり
となるのでF0=18.9>F(3,8:0.05)=4.07が成立し有意差があるとなります。
最後に因子Bが追加されても同じような考え方で対応できます。
また因子Aと因子Bが組み合わさることで相乗効果が表れる場合は、統計学では交互作用と呼び下記のようにして求めることが出来ます。
とはいっても考え方は同じなので、簡単にしか書きませんが交互作用の求め方は
- 同じ交互作用が発生する実験が2つ以上が必要(平均値を求めるため)
- 『4それぞれの水準の効果はいくらか?』で求めたように
「同じ交互作用の組合せの平均 -全実験値の平均 -A因子の効果-B因子の効果 」 が、その組合せの交互作用の効果となります。
余談になりますが実験計画法の成り立ちから全ての水準間の効果を合計した値や誤差の合計は必ず0になります。
具体的には例えば図9.1の場合、水準間の効果の合計-4.5+0.5+0.5+3.5 を計算すると0になっています。
また誤差のばらつき例えば水準20の場合を例にすると0+1+(-1)も0になる。
このことを利用して実験数を減らして実験を計画するというのが実験計画法 になります。