3.推定
母集団と標本
最適なボールペンを作るために正確な日本人の親指の平均長さが知りたいとします。
しかし、日本人全員の親指の長さを測定し平均を出すことは不可能だ ということは誰でも 分かります。
なぜなら学校に行っている小学生の平均身長でさえ、算出には多くの労力と時間が必要ですし、それでさえも測定漏れは間違いなく存在しているからです。
つまり真の日本人親指平均長さを知ることが出来るのは神様しかいないのです。
そうは言っても私たちは良いボールペンを作るためには正しい親指の平均長さがどうしても 必要と仮定します。
その場合、親指平均長さを推測するしかないです。
推測するにはどうした らよいでしょうか。
普通私たちは、かたよらないように何人かの日本人を集め、その人たちの 実際の親指長さを測定し、その結果を基に真の日本人親指平均長さを推測するのではない でしょうか?
統計学も全く同じ考え方で推測します。
そうはいっても統計学では少々言葉が変わります。
推測することを推定と言い日本人全員のように調査対象全てをもれなく集めた集団これを母集団と言います。
そしてこの母集団だと大きすぎて測定が困難なため、この母集団から何人かの日本人を集めて (この集められた日本人をサンプルもしくは標本という)集団をつくる、この集団を標本と 言います。(今回は20名の人間の親指長さを測定したとします。)
つまり、集団は2つできるのです。
そして工程能力ではで勉強したように個々のデータではデータ数が多すぎ役に立たないので、普通、平均と、標準偏差を用いて集団の特性を表します。
結果、先にも述べたように集団は2つあるのだからそれぞれの集団にも平均標準偏差ができてしまいます。
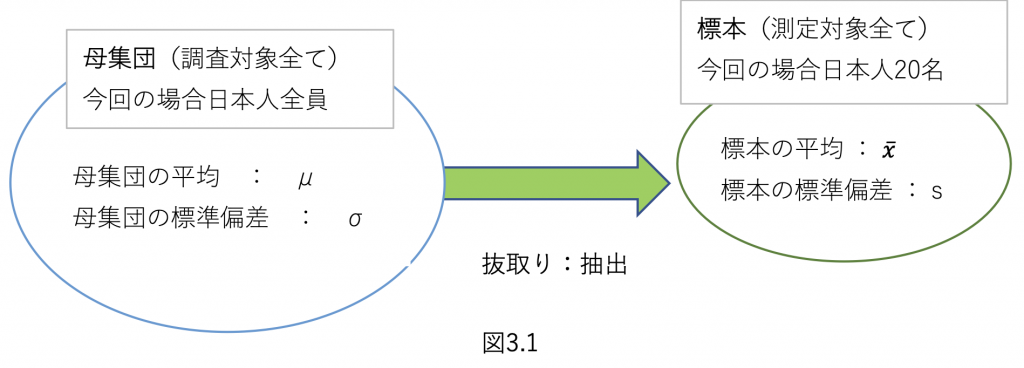
これらの平均 標準偏差は混同しないように、通常母集団の平均はμ(母平均という) 母集団の標準偏差はσ(母標準偏差) 標本の平均は 𝑥ҧ (標本平均)標本の 標準偏差はs(標本標準偏差)で表すという約束事があります。
この関係を図示すると図3.1のようになります。
2 点推定
さて、それぞれの関係が分かったところで母集団の平均を、与えられたデータつまり標本と して集めたサンプルで測定した値で推定します。
何度も言いますが母集団の真の平均の値は 全てを測定する必要があるので分かりません。
しかし、それでも標本の平均をもって、この値が母集団の平均値に近いのではつまり代用が可能なのではと考えることが出来ます。
実際、標本の平均をもって、これを母集団の平均と推定することがあります。
そしてこのように一点の値で推定することを点推定と言います。
具体的には、平均は

標準偏差は工程能力とはで説明したように下記不偏標準偏差を使います。

説明が遅くなったのですが、μとσの上に付いている記号「^」は「ハット」と読み、 推定値であることを示します。
ところで、この点推定ではあくまで標本平均の値であり母平均とおなじではありません。
具体的には標本平均が6cmで母平均が6.1cmということはあり得るのです。
しかし真の母平均の値は1項に書いたように実測が困難で不明な事が多いです。
そこで5.8~6.2cmの中に95%の確率で存在すると推定することがあります。
このように幅をもって推定することを区間推定と言います。
しかし、この区間推定を理解するには次から説明する3項(正規分布)の勉強が必要です。 (点推定さえ分かれば区間推定など必要ない と思うでしょうが、この考え方が次の章の検定の基礎に なり、魔法みたいなことが出来るようになるので難解でしょうが頑張って理解することが必要です。)
正規分布と標準正規分布
工程能力とはにも書きましたが、例に挙げたような親指長さなどのデータを集め縦軸に頻度 (正確には確率密度)横軸に大きさのグラフを作成し、面積=確率 となるグラフを作るとします。
当然、このようなグラフの場合、平均値の値を取る頻度(確率密度)が最も多く、平均値から離 れるにつれ頻度(確率密度)が減っていくつまり釣鐘のような模様ができるといいました。
このようにデータを集めて出来る模様を分布といい、釣鐘状の分布を正規分布といいます。
余談になりますがなぜ模様が出来るかというと根底に何らかの法則があり、その法則に従うために模様が出来ると考えられています。
そして、正規分布は(1.6)式で表されるのでした。

特に平均0 分散1をとる正規分布を標準正規分布と言い(3.1)式で表されます。

(𝜇 = 0、𝜎2 = 1を(1.6)式に代入して算出)
平均0 分散1にすると若干 式が簡単になり計算が容易になることが分かると思います。
また(1.6)式,(3.1)式からも分かるように正規分布は2つの項目(平均と分散)で形が決まってしまいます。
逆に言えば平均と分散さえ分かればどのような正規分布か分かるということです。
そこで変数𝑋で作られる正規分布 平均𝜇 分散𝜎2はX~𝑁 𝜇, 𝜎2 で表します。
話が少しずれました。
話を元に戻します。
標準正規分布にして式が簡単になったといっても電卓では計算は難しいため、すでに計算されている表を使います。
この表の事を正規分布表と言い2つの種類があります。
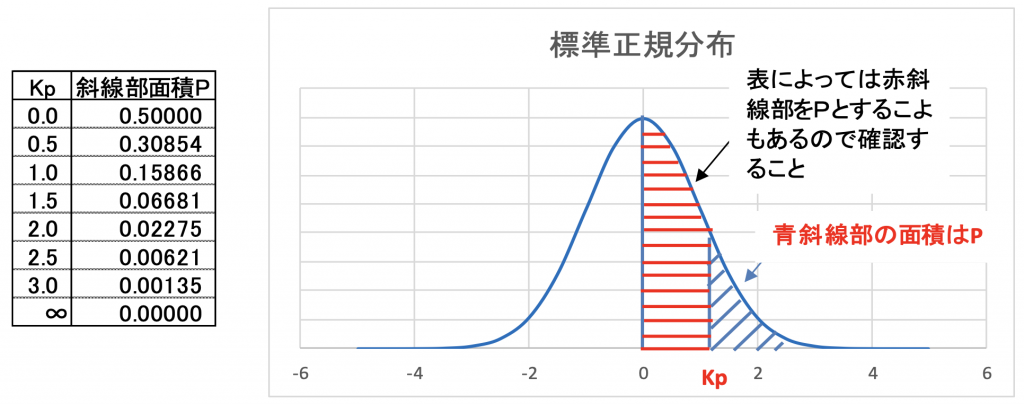
1つは図3.2にあるようKpを中心とした正規分布表です。
例えば、Kpの値が0.5の時。
面積Pはいくらの値を取るかを調べたいとき使用します。
(図3.2よりKp=0.5の時 Pは0.330854を取る)
もう一つの正規分布表は表3.1にあるようにPを中心とした正規分布表です。
面積が0.05の時(5%の時)取りうるKpの値はいくらかを調べたいときに使用します。 (表3.1よりP=0.05の時 Kpは1.645を取る)

図3.2のKpの値は0.5の幅でPがどのような大きさになるか示していますが、もし幅が0.001で 記載されている図3.2の表があった場合、表3.1は不要になります。
しかし、その場合あまりにも大きな表になり検索するのも大変なため通常は2方向の(KpとP)のよく使う値のみを記載した2つの表を使う方がより良いです。
ところで図3.2や表3.1の正規分布表は平均が0 標準偏差が1の場合 取る値を示しているのであり 普通の正規分布は 平均が0 標準偏差が1ということはまずないです。
それでは 図3.2や表3.1は役に立たないのでしょうか?
そんな事はありません。
次で紹介する(3.2)式を使えばどのような正規分布も標準正規分布に変換することが出来るのです。

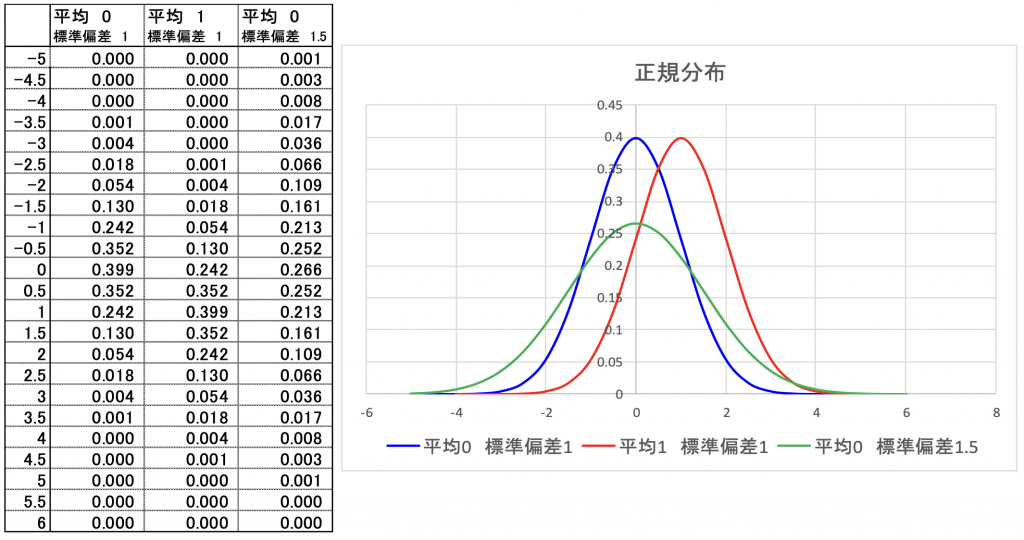
何故 このような式になるか証明は難しいのですが、下表のように青線で標準正規分布を書きます。
次に平均が1だけ変化した場合を赤線で書きます。
するとこれは青線よりグラフが1(平均)だけX軸方向に移動していることが分かります。
つまり 平均分を減算すると標準正規分布になるのです。
次に標準偏差が1.5だけ変化した場合を緑線で書きます。
これは青線より1.5倍すそのが広がっていることが分かります。
つまり標準偏差分を除算すると標準正規分布になるということです。
この事を式で表したものが(3.2)式になるのです
余談になりますが、(3.2)式を使うと次のような問題を解くことが可能になります。
(問題)いま日本人男性の平均身長が170cm 標準偏差が6に従う場合、176cm以上の身長の人 は何パーセントか?
(解答) これを解くには(3.2)式を使用して平均170 標準偏差6の分布を標準正規分布に変換します。
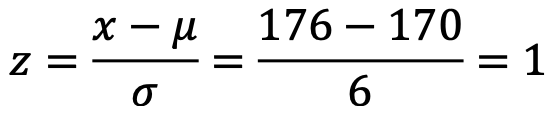
標準正規分布になれば、すでに計算されている正規分布表が使えるので、図3.2から1は 0.15866なので15.9%が176cm以上であるとなります。
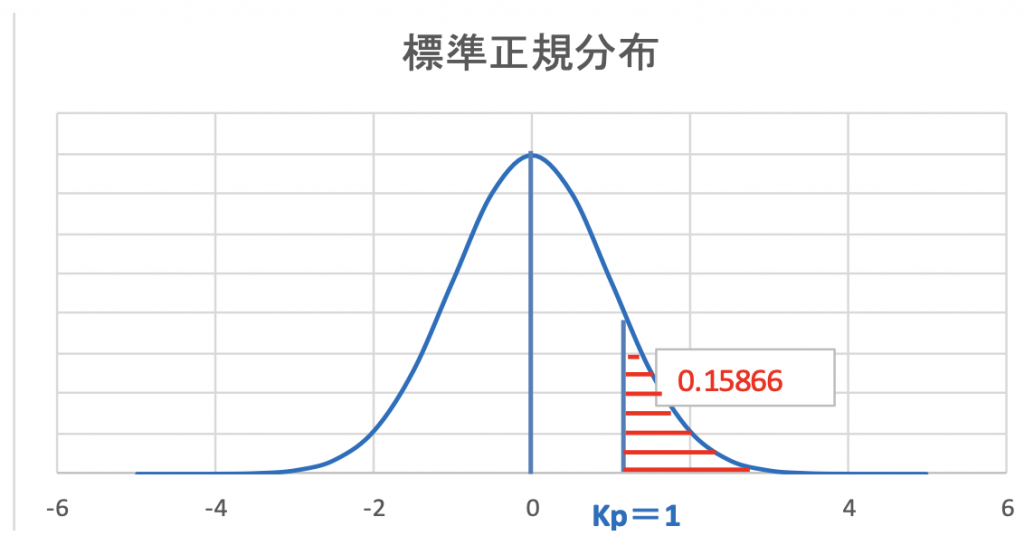
このような問題を解く場合は最初は図3.4で示した関係を書いた方が理解が容易になると思います。
もう一つ覚えてほしい公式があります。
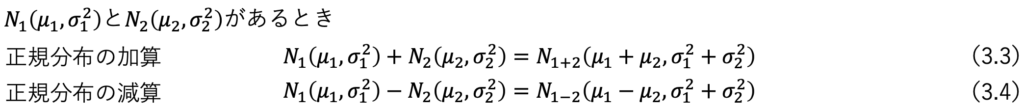
の関係があります。
証明は省略しますが、それぞれの正規分布を加算(または減算)すると平均はその計算どおりの値 になるがばらつきである分散は加算しても減算してもばらつきは組み合わせ分増える という感覚的に納得する計算式ではないでしょうか。
また、分散は単純に加法していくことが出来ますが、標準偏差は分散のように単純に加法することはできない事に注意してください。
また平均及び分散には下記にあるような関係があることは 知っておいてください。
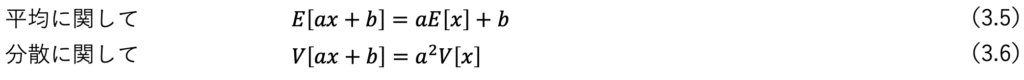
区間推定
第1章5項で少し説明したのですが標本Xの取りうる範囲が

変数Xはμ-σ~μ+σの範囲で68.26% (※1 68.26の算出理由は後述)
そしてμ-2σ~μ+2σの範囲で95.45%(95.45の算出理由も後述)
μ-1.96σ~μ+1.96σの範囲で95%の確率でその事象が起きます。(※2 1.96の算出理由も後述)
- ※1 68.26 95.45の理由
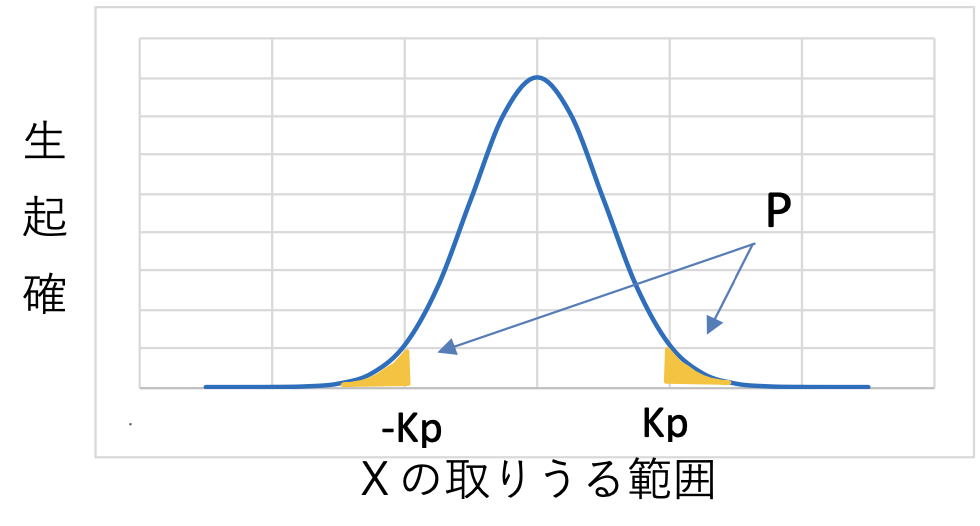
図3.5にあるような関係があります。
つまりXの取りうる範囲が-Kp~Kpの場合その生起確率は100%から2つの黄色の面積Pを引いた値になるのです。
また どのような正規分布でも3.2式で標準正規分布(平均0 標準偏差1) に変換可能なのでμ-σ~μ+σはμ=0 σ=1を代入して 図3.5 -1~1の値となります。
図3.2よりKp=1の場合Pは0.15866なので 100%の確率 つまり1から 2つのPの面積を引いた値 1 – (2 X 0.15866) = 0.68268 となるのです。 - ※2 1.96の理由
68.26算出理由と同様 図3.5のような関係があります。
そして95%の範囲を求めたいのだから黄色の面積の合計が5%になる必要があります。
また黄色の面積は2つあるので5%の半分 2.5%つまり0.025が黄色の面積になるKpの値は表3.1の0.025の欄から1.960になるのです。
別の言い方をすると、無作為にサンプルを取るとそのサンプルの95%はμ-1.96σ~μ+1.96σ の範囲のものということで、これを式にあらわすとμ-1.96σ≦X≦μ+1.96σとなります。(3.8)
これを 『μ-1.96σ≦X』 と 『X≦μ+1.96σ』 に分けてμについて解き、再び結合させるとμ の取りうる95%の範囲 X-1.96σ≦μ≦X+1.96σ が計算されます。 (3.9)
でも、私たちは母平均の推定が目標の為、サンプルは1個ではなく複数個で推定することが多いです。
いきなり複数個の推定は難しいので最初は2個を考えます。
さて、3項の終わり式3.3で正規分布の足し算を勉強しました。
この母集団からサンプルを2個抽出すると、その分布は
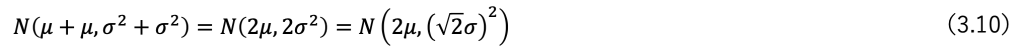
となり、n個抽出すると 下記のような式になります。

n個抽出するのは平均を出すためだったので、この分布を平均 つまりnで除算すると

となります。
この分布がn個抽出して平均を計算した際に出来る分布 つまりn個の平均が取りうる確率分布となります。
この分布は1個の抽出で計算したX-1.96σ≦μ≦X+1.96σ (3.8)式と同様に計算することができ、 その値は

となります。
意味もn個の標本平均を求め母標準偏差σが分かれば95%の確率で存在する母平均μ の範囲は(3.13)式のようになるということです。
つまり、母標準偏差が分かっている時は正規分布で 区間推定ができるのです。
ところで、母標準偏差が分かっていれば(3.13)式で問題ないのですが、 母平均を推定しようとしている時に母平均よりも算出が難しい母標準偏差が分かっているという事はあまりないと思います。
そこでσが分からない場合はσを最も適切に表す点推定で使った

をつかいます。
それでも、σとsは違うのだから・・・3.13式を単純に3.14式のように置き換えるのは間違いではないのかと思うでしょう。

事実そうです。1.96は標準正規分布から算出した値ですが、母標準偏差が不明な時は標本標準偏差sを使っても誤差があると考え、1.96よりも大きな値をとります。
つまり、母標準偏差が不明な場合は正規分布を使うのではなく誤差を含んだ分布『t分布』で値を 出すのです。
t分布の算出の説明はしませんが母標準偏差が不明な時はt分布を使うと覚えてください。
そうはいってもt分布とはどのような分布でしょうか?
図3.6に標準正規分布とt分布を示します。
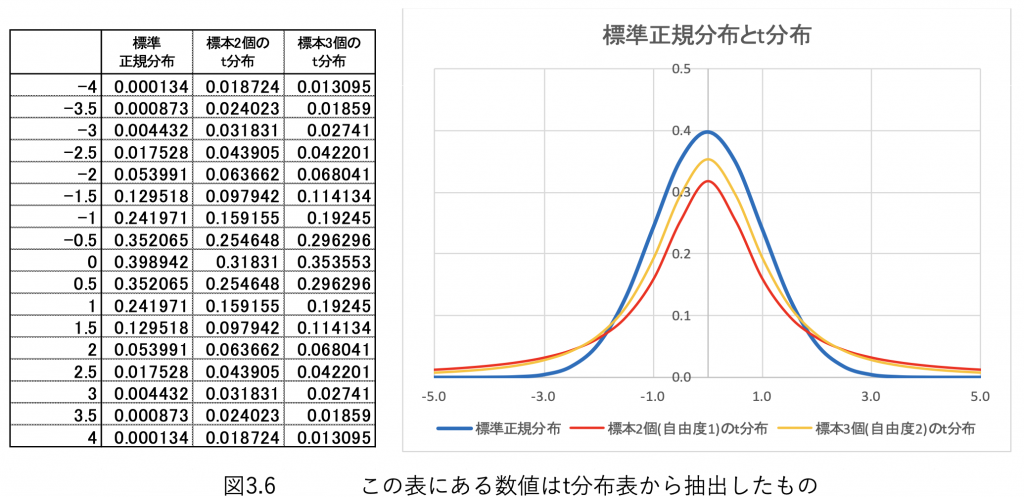
図3.6を見ても分かりますように標本が少ないと平べったい、つまりばらつきが大きい分布になり 標本が無限大になると正規分布となります。(一般にはn=30を越せば正規分布の値と大きな相違が 無いと言われます)
また通常t分布は標本数ではなく自由度をもとに書かれており自由度とは標本数-1の値となります。
この表から標本数が3個の場合で母平均を95%の確率で求めたいときは既に面積が計算されたt分布表(図3.7)を使います。
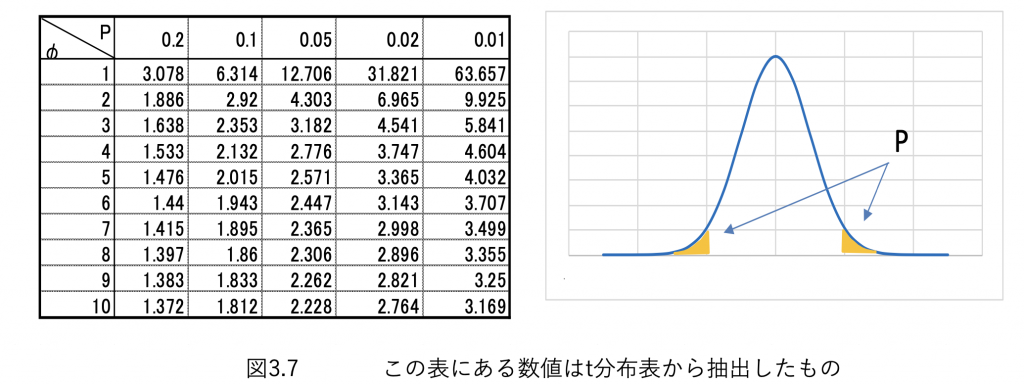
すると標本数3(自由度φ=2)とP=0.05の交わる数字を読み取って4.303を1.96の代わりに使用し(3.15) となり、見事 標本3個では95%信頼できる区間が(3.13)式と比べ大幅に広がったのでした。

繰返しになりますが、母標準偏差が分からない場合は標本標準偏差を代用する代わりに正規分布は 使えなくなりt分布を使って区間推定をするという事です。
補足
ここで、補足説明として抜き取りに関する決め事を2つ紹介します。
1つは、『大数の法則』といわれるものです。
この法則は物事は必然の方向に動く というものです。
具体的にいうとサイコロを3回ふって3回 とも1の目が出ることはまれにあるかもしれません。
しかし、実験を100回 1000回と増やしていけば必然の方向つまり1/6の比率である16回 166回に近づいていくというものです。
もう一つは『中心極限定理』です。
その説明の前に忘れているかもしれませんが、もともとは1項にあるよう親指の平均長さを調べる ため20人の日本人を集めその測定を行ったのでした。
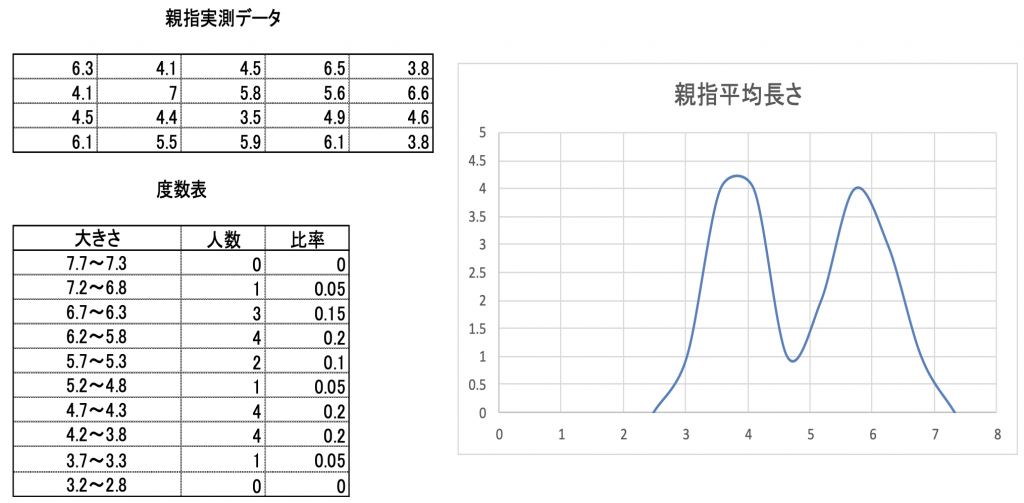
その結果は、親指実測データにあるものであり、それの度数表をつくりグラフ化したものを図3.8に 示します。
大きさは正規分布に従うと言っていたにも関わらすこのグラフは釣鐘のような形ではなく、山がふたつあるような形になり正規分布に従うとは言えなくなりました。
その理由はサンプルの中に男10人 女10人がおり、男の正規分布と女の正規分布が重なったから と考えられましたが、そのことは多く触れません。
参考までに『法則』とは経験や実験などからよくそういう事実があると認められたもので証明されていません。
『定理』とは、定義などを論理的に積み重ねることで証明され、かつ有用と認められたもののことです。
上記の場合、サンプル数が少なくこれを母集団というのは問題がありますが、定理の説明の為これを母集団と考えてほしいです。
そのため、これはサンプル数が20ではなく何万とあって構成された母集団(平均μ 標準偏差σ )と考えてください。
この母平均μをサンプルを使って推定するのですがこの時
1 母平均を推定するのであるから、母集団は正規分布でなくても構わない。
⇒
特殊な場合を除き、どのような分布でも問題はない
2 母平均を算出するために多くの標本の集団を作った結果、多くの標本平均ができる。
その多くの標本平均の集団は正規分布に従う。
⇒
たったひとつの母平均算出のために作られた多くの標本平均の集団は当然母平均に近いものが多く現れ、離れるにつれ少なくなる釣鐘状(正規分布)になる。
3 多くの標本平均で作られた分布は、
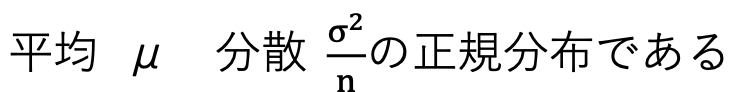

中心極限定理を図3.9に示します。
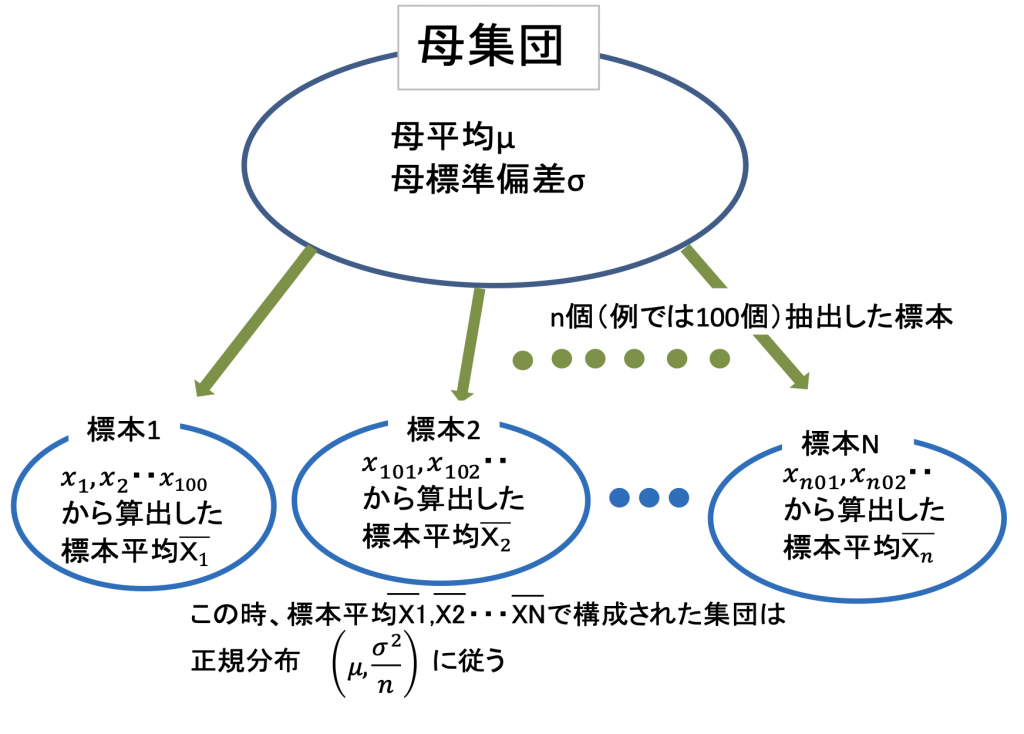
この中心極限定理は、多くの事柄が正規分布に従う拠り所をこの定理に求めている証明になるのはと思われています。