8.相関
はじめに
加熱時間と強度を測定すると表8.1のようになったとします。
この表をグラフで打点すると図8.1のようになりました。(単位省略)
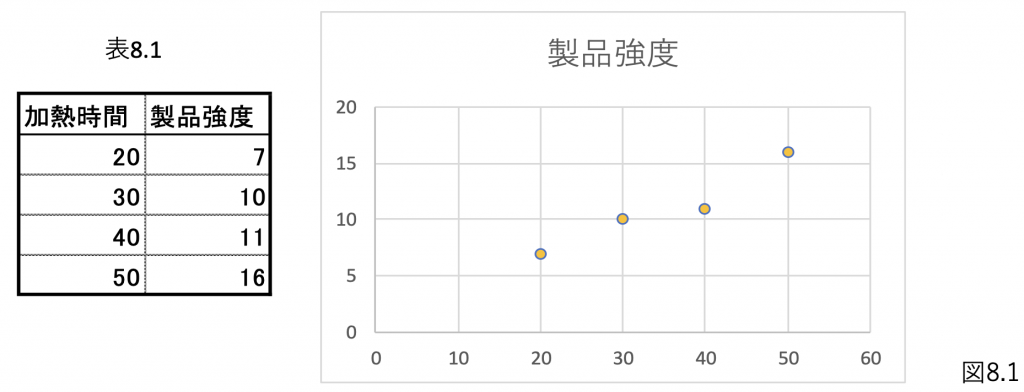
図8.1を見ていると図8.2のような線が背後にあるように見えないですか?
そして、この線のように加熱と強度の関係があるとしたら実験していない60時間での強度も推測できるのではないかと思えませんか?
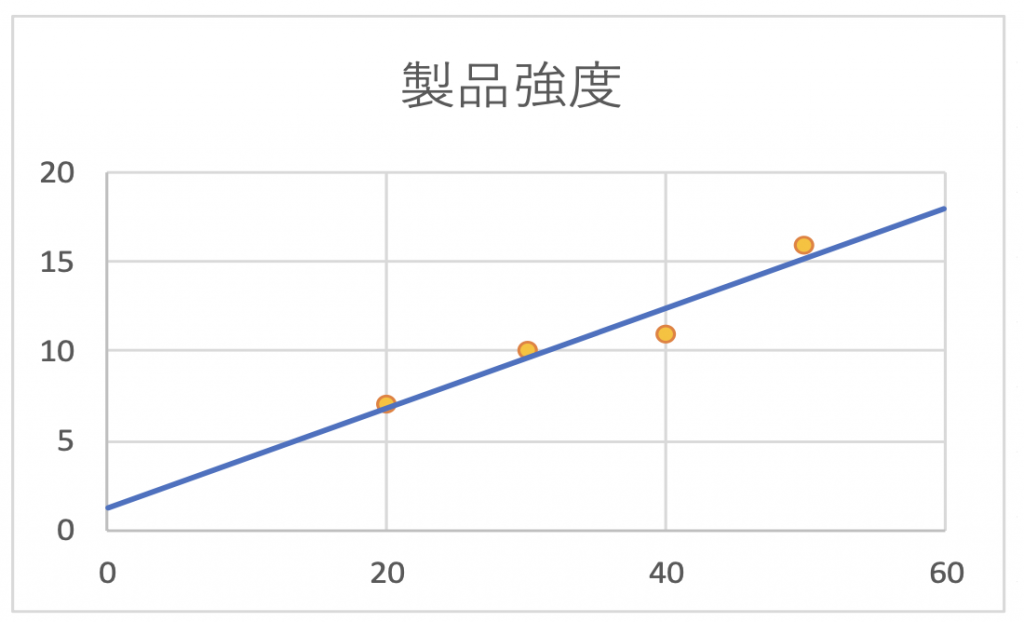
図8.2
しかし、線が見えるとはいえ人によっては図8.3の赤線のように引く人もいるかもしれません。
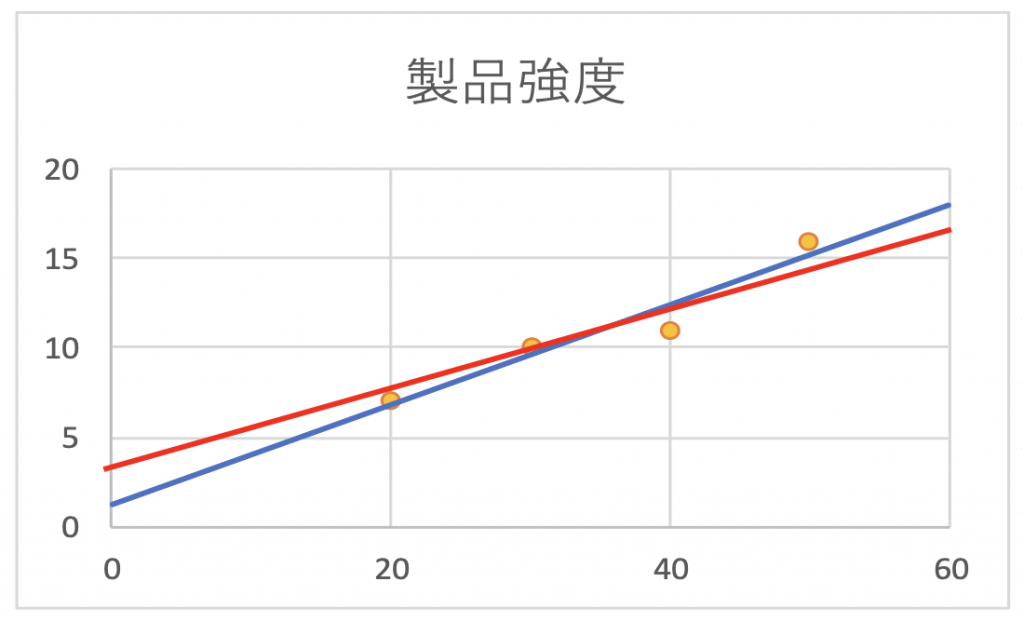
図8.3
どちらがより正確な線なのでしょうか?
実は、数学的には偏微分という方法などを使って線と打点との距離を最小にするような正しい線を引く方法が分かっています。
(距離が最小ということは『打点の座標 – 線の座標』を計算するといいのですが、これだとまたプラスやマイナスの符号がつくので『打点の座標 – 線の座標』を2乗して最小にします。 そのためこの方法を最小2乗法と呼びます)
回帰直線
直線の式はY=aX+b(a,b:定数 Y,X:変数)で表すことは中学生で勉強しました。
そして偏微分などを使用するため説明は省略しますが数学的正しい直線を構成する定数a、bは下記の式で求められます。
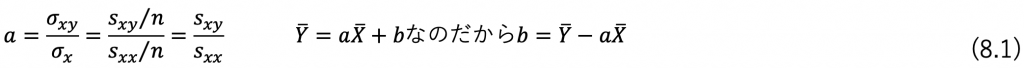
すなわち、傾きaはxとyの分散(これを共分散と言う)をxの分散で割ったもの となります。
また、𝑆𝑥𝑥 を𝑥の平方和 𝑆𝑦𝑦 を𝑦の平方和 𝑠𝑥𝑦 を𝑥と𝑦の積和と呼びます。
ここで、新しく出てきた共分散と平方和・積和に関して簡単に説明します。
分散は次式で算出されます。
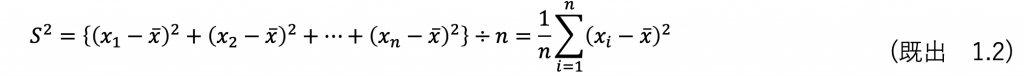
それぞれのデータから基準とする平均値がどれだけ離れているか引き算し求めます。
そして、その値を2乗することでプラスやマイナスの符号をかき消し、そしてその和をデータ数で割ることでデータ数の増減に対応ということでした。
そして共分散は
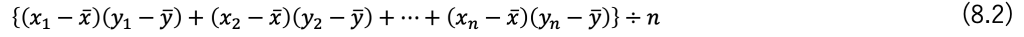
で求められます。分散はそれぞれのかっこを2乗するのですが共分散は2乗しないかわりにそれぞれを掛け合わせるのです。
また共分散では2乗しないのでマイナスになることがありますが、これはxが増えるとyも増える場合はプラスになり逆にxが増えるとyが減る場合はマイナスになるということです。
また、すでに2項 補足説明で説明していますが、分散はまともに計算すると計算が困難なため次式に示すよう変換して算出します。

また、その調子で平方和や積和も下記の様に変換します。
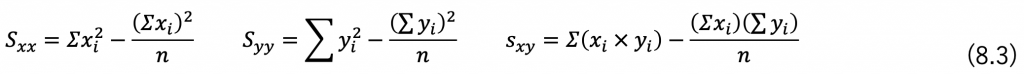
(分散と平方和はデータ数で除算しているかいないかだけの違いだけなので分散の式にデータ数を乗算すると積和になります)
線を引くことはできましたが、変数XとYの関係はどれくらい関係があるのか (≒にあてはまるのか)は相関係数 という次式で紹介する数式で示せます。

それでは、それぞれの関係を見てみます。
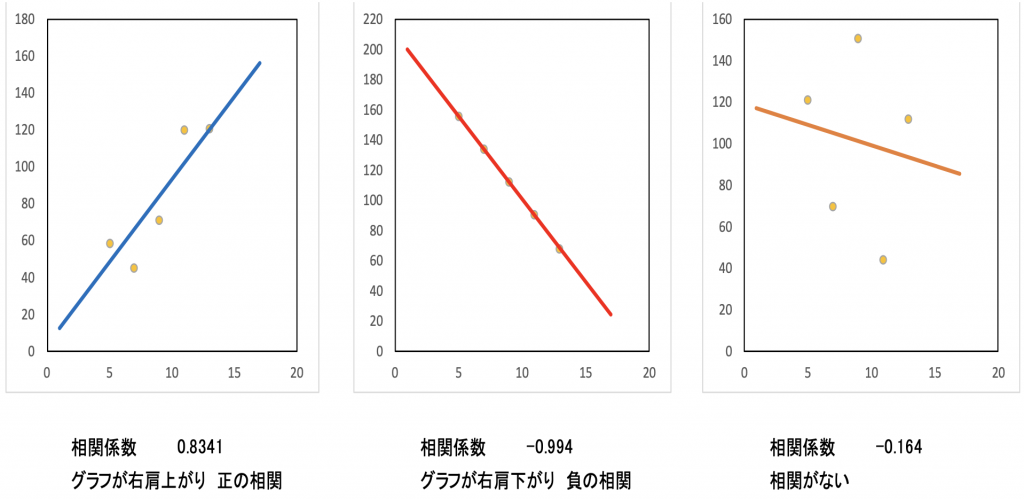
図8.4
打点と線が一致に近いと相関係数の絶対値は1に近くなっていることが分かると思います。
相関係数の値は-1から1の間を取り0に近いほど相関がないとなります。
そして、相関係数がプラスの値を取るときグラフは右肩上がりになり正の相関があるといい、逆にマイナスの値を取るときグラフは右肩下がりになり、負の相関があるといいます。
また、相関係数はグラフの傾き方向は分かるのですが、グラフとどれだけ一致しているかはマイナスの値をとるため難しいです。
そこで相関係数を2乗したものを寄与率という認識で次式を覚えてください。
(この考えは間違ってます。下記に正しい考え方を書きますが 今は必要ないです。)
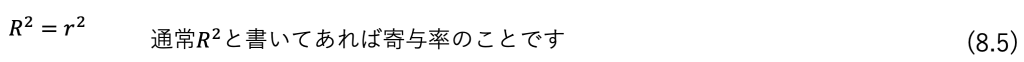
寄与率について
回帰直線y=ax+bで表せるとき xは説明変数 yは目的変数と言います。
そして、目的変数の動きは「回帰直線で説明できるもの」と「説明できないものつまり誤差」 に分けることが出来ます。
目的変数xの平方和のうち「回帰直線で説明できるもの」の割合を寄与率というのです。
yのばらつき𝑅2%がxのばらつきで構成されているという事です。
逆の見方をすれば 1 − 𝑅2 % がx以外の他の原因でばらついているという事になります。