7. 抜き取り検査
はじめに
検査は全数行えば良いということはないです。
検査してしまうと破損して使えなくなる製品もあるからです。
検査すると壊れてしまうような検査を破壊検査と言います。
破壊検査が必要な場合は、当然ですが全数調べるのではなく抜き取り検査を行います。
とはいえ、例えば1000万個に1個の不良が入っているロットがあったとします。
ここから1個抜き取り検査をし、偶然にも不良の1個を取ってしまいました。
このロットを 100 %の不良率と判断してよいでしょうか?
正解を知っているので間違っているとなりますが、偉い学者はこの問題をどう対応したのか説明していきます。
OC曲線
破壊検査が必要な製品なので、不良率1%以下のロットは合格ロットとするという取り決めがあったとします。
この場合、500個製品を作り、そこから100個抜き取り検査をした結果、不良品が2個あったとします。
この時、このロットは不良率2.04%(2÷(100-2))なので不合格と考えてよいのでしょうか?
実は抜き取り検査の場合、真のロットの不良率が何%かは分かりませんので先の命題は成り立たないです。
先の例でいえば、498個良品2個不良品のような優秀なロット(不良率0.4%)であっても、100個抜き取りの中に不良品が2個含まれるということがあり得ます。
そして、この確率は先に勉強した2項分布の式を使えば算出できます。
具体的には498個良品2個不良のような優秀なロットから100個抜き取り検査をした結果、不良が1個以下になる確率は

で算出できるのです。
これを様々な不良率で計算していった場合、グラフが出来これをOC曲線と言います。
つまり、式(5.5)を使用し100個抜取をし1個NGが出た場合、真のロット不良率が0.2%の場合、0.983になる、0.4%の場合0.938になります。
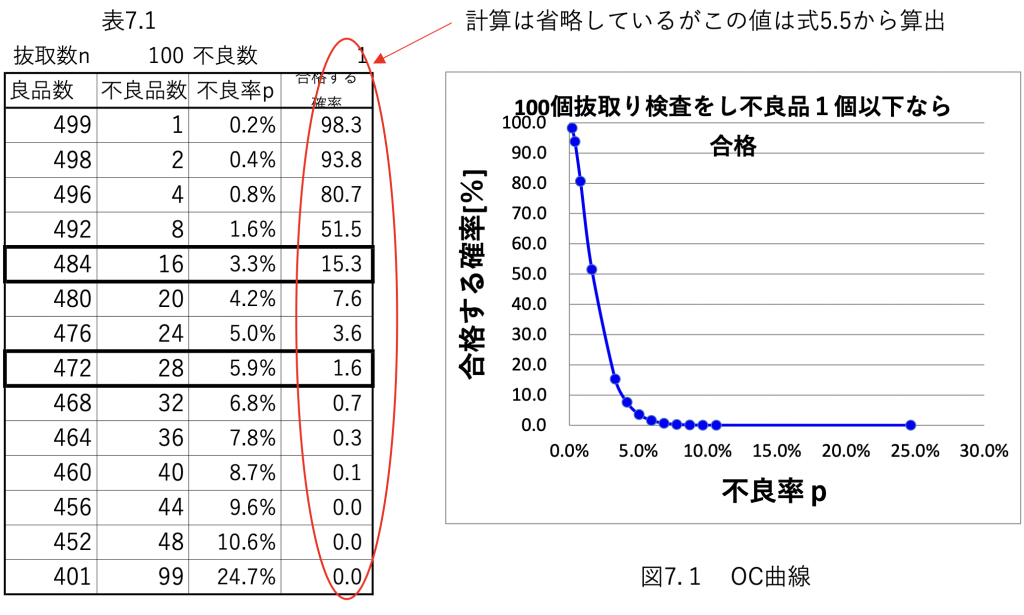
(表1.1参照)このように不良率を順々に増やしていきそれが出現する確率をもとめ一覧表にしたのが表1.1でそれをグラフ化したのが図7.1 のOC曲線となるわけです。
具体的には、表7.1を見てほしいのですが真のロット不良率が3.3%の場合(500個中16個不良品がある場合)でも100個抜取し1個NGという事が、15.3%ありえます。
同じことですが、真の ロット不良率が5.9%の場合(500個中28個不良品がある場合)でも1.6%の確率で100個抜取検査をし1個NGという事があり得るというのがこのOC曲線から読み取れるのです。
つまり、OC曲線とは表図1のように 100個抜き取り検査をして1個不良があった結果をどう見るかを一覧表にしそれをグラフ化したものです。
OC曲線の種類
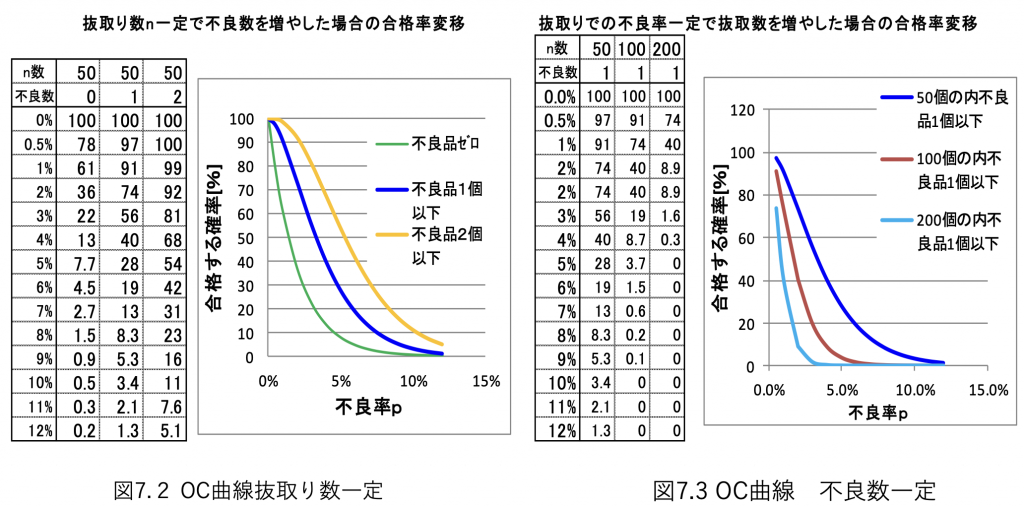
OC曲線は、抜取数と不良数で決定するため、どちらかを固定すると下記のように2種類のグラフができます。
当然ですが抜取数一定で不良数が多くなるほどOC曲線はなめらかになるつまりあいまいさが増えます。
同様に不良率が一定で抜取数を多くすればするほど正確な検査ができます。
OC曲線の欠点
OC曲線を作ることで、抜取り検査結果の信用度が一目で分るようになりました。
しかし、100個抜き取り検査をし1個不良が発生したロットの場合、不良率が3.3%のロットでも15.3%の確率で合格ロットと判定されると分かってもどうしようもないです。
とはいうものの100%の確率を求めると全数検査ひいては全数破壊になってしまいます。
仕方ないので5%の確率で正確ならばそのロットは合格であるとしたいと思います。
この時、5%の確率は2方向から見ることが出来ます。
つまり、本当は合格にもかかわらず5%の確率で不合格になる場合と本当は不合格なのにもかかわらず5%の確率で合格となる場合です。
この合格にも関わらず不良とされるのは生産者にとっての損でありこれを『生産者リスク』といいます。
そして不合格にもかかわらず良品として買わされるのは消費者にとって損であり、これを『消費者リスク』といいます。
そして場合によりけりなのですが通常、生産者リスクは5%、消費者リスクは10%とすることが多いです。
それは生産者リスクが高い、つまりロットアウトになる確率が高い場合、 生産コストが上がり、ひいては価格が上がり消費者も損するからです。
しかし、医療品のように人命がかかわる場合は逆に消費者リスクを低くします。
OC曲線の見方
4項で2方向の見方ができると書きましたが、OC曲線ではその2方向はどこに現れるのでしょうか?
具体的には図7.4のように消費者リスクはOC曲線の内側、生産者リスクはOC曲線の外側に現れます。
このことを実例をあげて説明します。
抜き取り検査の為、真のロット不良率は分からないが100個抜取りをして不良品が3個以下ならば合格ロットと判定するとします。
(くどいようですが抜取り検査の為、真のロット不良率は分かりませんが100個抜取りのうち不良が3個以下ならば合格ロットとするということは素直に考えると3%程度の不良までは許容しようと考えていると推察できます。ここでは話の便宜上、不良率3%までを合格ロット決めていると考えてください)
この時、100個の抜取り検査において本来なら不合格ロットであるはずの不良率7%のロットが 7.44%の可能性で不良数が3以下になると図4のOC曲線から読み取れます。
本来ならばロットアウトにすべきロットを確率の性格上、合格ロットの判定をしてしまう可能性があるということです。
つまりはロットアウトすべきものを消費者がβ%(OC曲線の 内側)の確率で買わされる(消費者リスク)があるということです。
次に100個の抜取り検査において不良率2%の本来ならば合格ロットにすべきロットも85.9%の確率でしか不良数は3個以下にならない。
言い換えれば逆の(100%-85.9%=14.1%)は不良数が3個を越えてしまうということです。
つまり合格ロットのはずのロットを確率の性格上、 不合格ロットの判定をしてしまう可能性があるということです。
そしてこの事は、本来ならば良品のものを生産者がα%(OC曲線の外側)の確率で廃棄させられる(生産者リスク)があるということです。
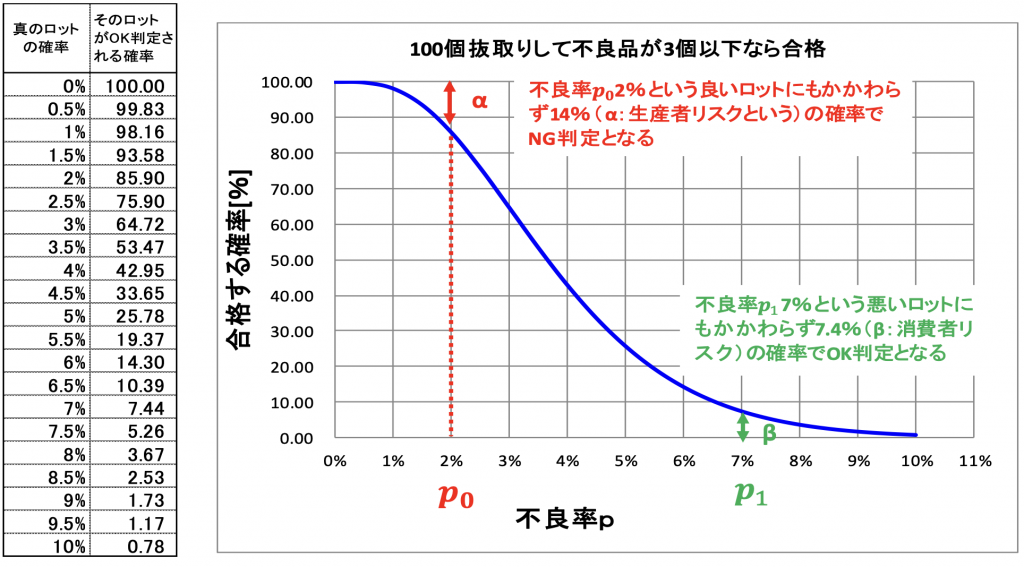
図7.4 生産者リスク 消費者リスク
抜取り検査表
OC曲線の見方は分かりましたが、結局 私たちは何個抜取りを行い何個不良品があったらロットアウトにしたらよいのか実作業に即した知識が必要です。
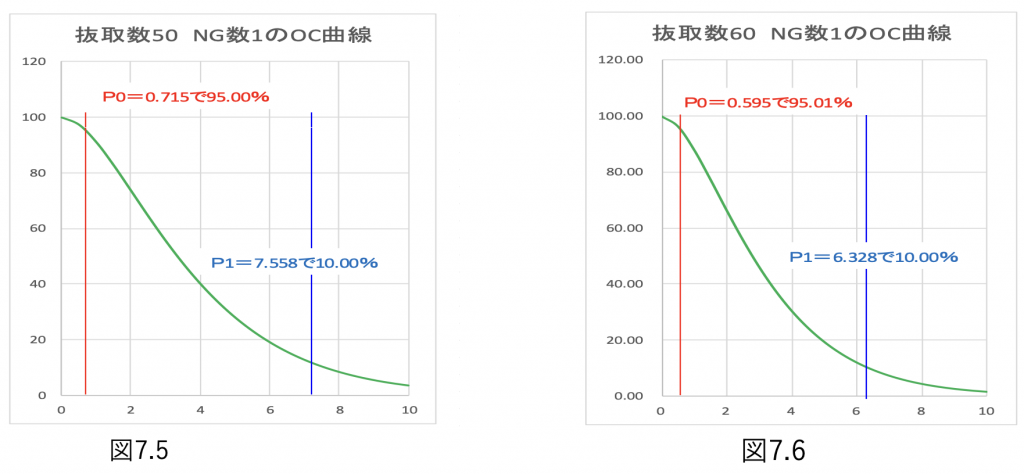
今ここで抜取数50 NG数1のOC曲線を見てみます。
(図7.5参照) するとP0=0.715で生産者リスク5%、消費者リスクP1=7.558 10%になることが分かります。
つまり、P0が約0.715% P1が約7.558を合格ロットとしたい場合、 抜取数50個でNG数1ならば、その基準を満たすという事になります。
同様にして抜取数60個でNG数1のOC曲線を見てみるとP0が約0.595%、P1が約6.328を 合格ロットとしたい場合、このような抜取をすればよいと分かります。(図7.6参照)
このようにして、10個に1個のNGがOKになるのは、次に15個に1個のNGがOKになるのは、と順々に計算していったのが図7.7のような計数基準型一回抜取検査表になるわけです。(赤矢印参照)
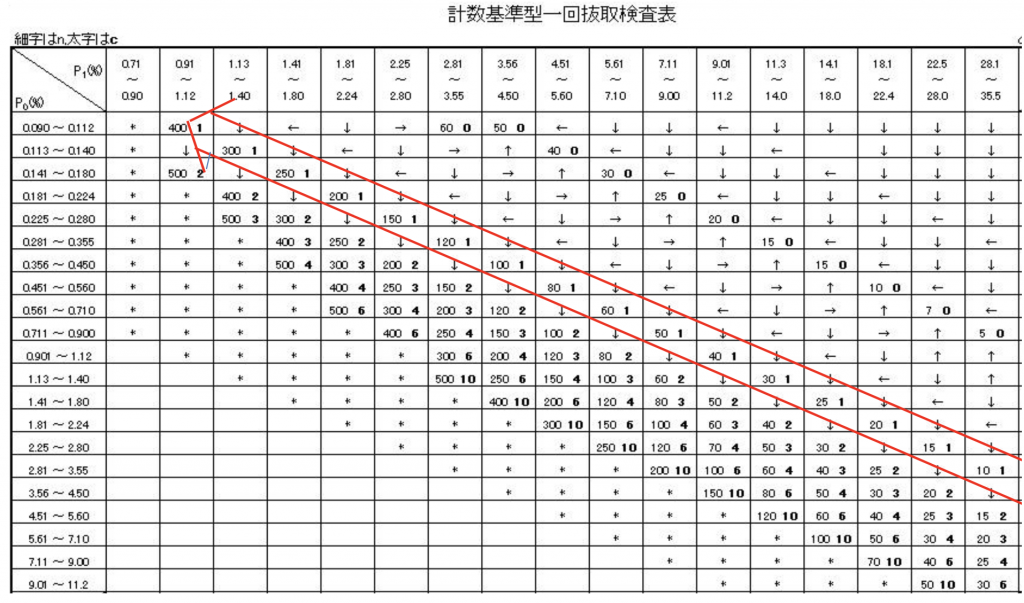
図7.7
具体的な表の読み方は図7.7は小さく読みにくいので図7.8にあるように抜き取ります。
そして生産者危険5%消費者危険10%で P0=0.15 P1=1を許容する場合、赤四角の範囲がそれに該当し、その交点である青丸の数字を読み取り500個検査して2個未満のNGであればそのロットは合格となります。
この時、2個の場合は合格になります。
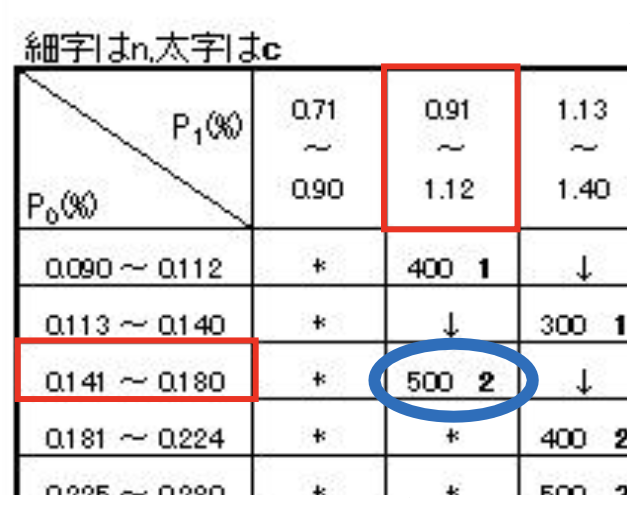
図7.8