5.二項分布 ポアソン分布

はじめに

今までは寸法などのように実際の値が測定できないものを扱ってきました。

20cmと書いていても実際の真の値は20.134562・・・・cmと際限なく測定していくことが出来るため正確な数値にはならないのです。

このように数えられないが故に量としてみる事柄を『計量値』といい、これらは今まで勉強してきた正規分布に従う事が多いです。

(連続型) そしてこれから不良個数などを扱うのですがこれは逆に不良個数2.5個などありえない事であり数えれるものを扱うため『計数値』といい、これらの分布は2項分布などに従うといわれます。(離散型)

2項分布前置き

2項分布とは2つの項目しかない分布の事です。

2つの項目とはコイン投げを例とすれば出てくるのは表と裏しかないと考える場合の事です。

コインが立ってしまったので縦があるなどとは冗談でも考えないのです。

アンケートでいえば『はい』と『いいえ』のみ『どちらでもない』は考えない。

このような2つの項目しかない事をあつかう事を難しい言葉で 『ベルヌーイ試行』といいます。

そして、この分布を勉強する前に場合の数と簡単な確率を知らないといけません。

場合の数

サンプル数nからk個抜き出すのを3つの抜き取り方でどのような場合の数があるか考えてみます。

まずはサンプル数nを全部抜き出す場合です。

A,B,C,Dが入っている箱から4個全部抜き出す場合、順序も考慮すると何通りあるでしょうか？

これをとくには図5.1のように全部羅列していきます。

すると右端にあるように4X3X2X1通りあると分かります。

このようにn個の異なるものを1列に並べる場合の種類の総数を計算するには、『1 から nまでのすべての整数の積』を計算する必要があります。

そしてこの計算をn!(かいじょう と読む)』で表します。(5.1)

A,B,C,Dが入っている箱から3個抜き出す場合 順序も考慮すると何通りあるでしょうか？

これも図5.2のように全部羅列していきます。

すると右端にあるように4X3X2通りあると分かります。

これは図1から抜き取り数3個分のみを抽出した図であると分かります。

逆にいえば下半分、つまりnから抜取り数kを差し引いたもの(今回の場合4-3=1 最後の1段)は削除されているのです。

このようにn個からr個抜き出した場合の総数はn-kの段を削除するため

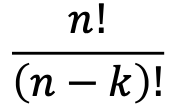
で計算され、このことをnPkで表します。(PはPermutation順列の意味)

A,B,C,Dが入っている箱から3個抜き出す場合 順序を考慮しない場合何通りあるでしょうか？

これは、先の3.2順序を考慮した組み合わせ数から順序を考慮してできる組み 合わせ数を除いたら計算できます。

順序を考慮してできる組み合わせ数は3.1で求めた場合の数だけあるので、この場合k! となります。

したがってn個からk個抜き出した組み合わせの総数(ただし順序は考慮しない)は

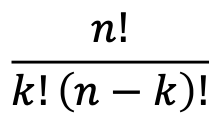
で計算され、

このことをnCkで表します。 (CはCombination組み合わせの意味)

確率

今表が出る確率が30%裏が出る確率が70%のコインがあったとします。

(表と裏しか出ないのだから当然、表が30%の確率で出るなら裏は100%-30%の70%)

この場合、表⇒裏が出る確率はいくらか

と言う計算を行うとすると図5.4のような経路を通ると分かります。

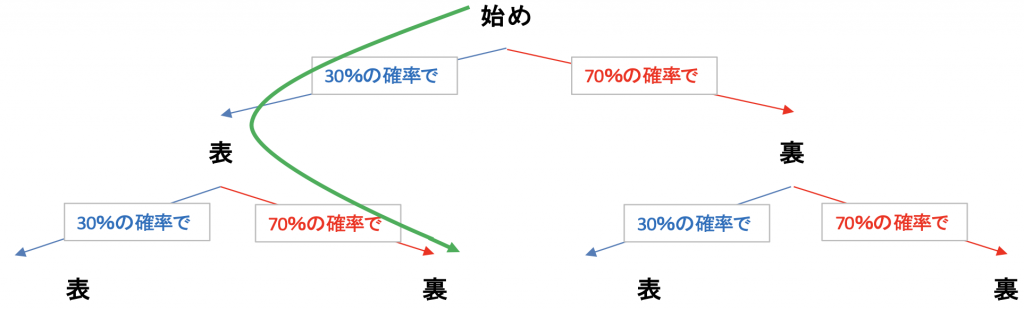
つまり、30%の道を最初に選び次に70%の道を選んだということです。

したがって、このように出る確率は30%X70%=21% となるのです。(5.4)

2項分布

ようやくここまで来ました。

例えば30%の不良率の箱から10個製品を取り出したとします。

この時、不良数が2個の確率は いくらになるでしょうか。

このような事例を扱うのが2項分布でこの章で勉強したことを総動員して計算してみます。

まず、10個のうち2個が不良になる組み合わせ数を計算します。

場合の数で勉強した

これだけの場合の数のうち不良率30%を2個、良品を8個取る道筋は

となります。

この2つを組み合わせたものが10個抜き取り検査をし2つの不良になる確率です。

• n:抜取り数(試行回数)
• p:確率(生起確率)
• k:pの確率が起きる回数

再度書きますが、

• PはPが起きる確率
• kはPが起きた回数

そして

• 1-PはPが起きない確率
• n-kはPが起きない回数

となります。

となり、これを2項分布と言います。

2項分布の特徴

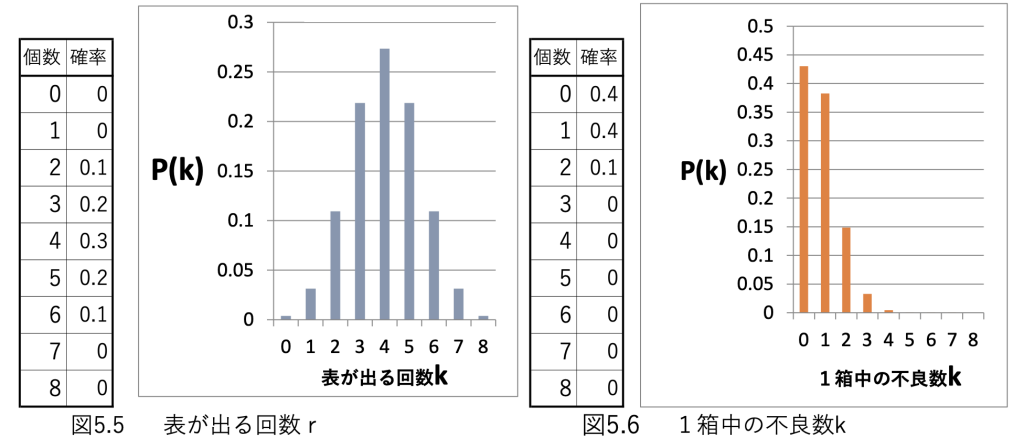
2項分布の式が分かったのだから、グラフを書いてみます。

一つはコイン投げのように表と裏が出る確率が50%の時の1個、2個・・・・の確率 → 図5.5参照 もう1つは不良率が10%の箱から8個取出し不良数が1個、2個・・・・の確率 → 図5.6参照

(参考)

図5.5のコイン投げを8回行って3回出る確率は0.2となっていますが、その計算式は

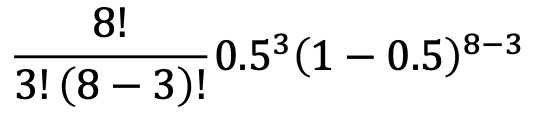
で計算され0.21875となります。

ところで、50%の確率の時の分布が正規分布に似ていると思いませんか？

数学的にいえば、二項分布の式でnを極限まで大きくしたとき正規分布が作られるそうです。

そして 二項分布の平均と分散は下記の公式で示されます。

E[X}=np (5.6)

V[X]=np(1-p) (5.7)

平均の式npは、例えばコイン投げを8回行えば表は50%の確率で出るのだから8×0.5=4回 (つまり8回投げれば表は平均4回出る)で計算されることは直感的に理解できると思います。

2項分布の欠点

2項分布には大きな欠点があります。

例えば200! この計算になるとエクセルでも算出できない375桁もある大きな値になるのです。

エクセルでさえ計算できない値を取り扱うにはどうしたらよいでしょうか？

前項6でわざわざ確率50%と10%で起きる場合のグラフ2つを紹介しました。

10%のものはn数が小さいためはっきりした特徴は出ないのですが、それでも起きる確率が小さくなればグラフの形が大きく変わるのが認識できると思います。

一般的にn数が大きく起きる確率が10%〜90%のように大きい場合、正規分布表を用いておおよその値は算出できるとされています。

(90%以上起きるということは起きない確率が10%以下になる ということ)

数学的に言えばnp>5もしくはn(1-p)>5が成立すれば正規分布表を用いて算出された確率を代用しても大きな相違はないとされています。

そして起きる確率が10%以下でかつn数が大きい場合、次に示すポアソン分布で近似値が算出できます。

つまり、まれに発生する事象を扱うときは、階乗計算(!)があまり必要のないポアソン分布が使用可能となります。

ポアソン分布

ポアソン分布は下記の式で示されます。

λ:(単位あたりの)平均発生数

k:求めたい発生数(λとの単位を合わせる必要あり)

e:自然対数の底 2.718・・・

また平均などは下記の公式で算出されます。

E[X}=λ (5.9)

V[X]=λ (5.10)

ところで、この式を見て気付くと思いますが、n数(試行回数)やp(確率)が必要ないというすごい特徴があります。

つまり、単位あたり平均何回生じたかその事実さえ分かれば、それが2回発生する確率3回発生する確率が求めれるということです。

少しまとめましょう

2項分布 :不適合品数(不良個数)または 不適合品率(不良率)を扱う ⇒集まり(ロット)に対する個数を使う場合に使用します。

ポアソン分布 :不適合数(欠点数)を扱う ⇒一単位(1個)に対する個数を使う場合に使用します。

具体的には、広島県全体で年に宝くじの1等が平均1回当たるならば2回当たる確率は？とかです。

この場合λ=1 発生数は2なのだから

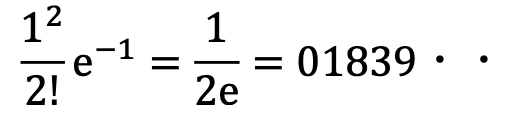
18.4%で生じると分かるのです。

勿論、2000回使用すると1回故障する機械がある場合、1000回使用して2回故障する確率などもn数が大きく生起確率が小さいためポアソン分布が使用できます。

具体的には、λ=1÷2000×1000=0.5 k=2

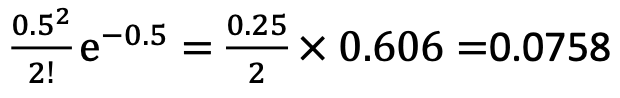
また、二項分布においてnp>5,n(1-p)>5を満たすとき正規分布の値を代用しても良いようにポアソン分布もλ>5を満たせば正規分布を使用して算出してもよいとされています。