2.補足知識
分散の計算方法
QC検定では実際に分散を計算することがありますが、

の計算は電卓で行うと時間がかかります。
最初に平均を計算し、そしてそれぞれのデータから平均を差し引き2乗それをすべて合計しデータ数で除算する。
電卓を使っても計算間違いしそうです。
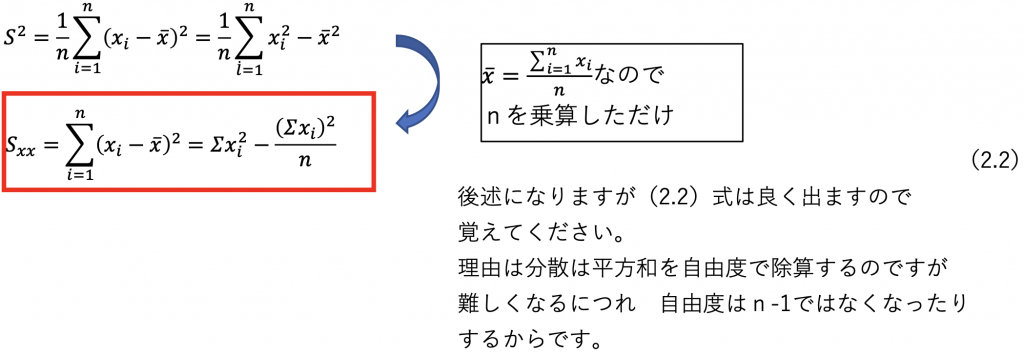
そのため
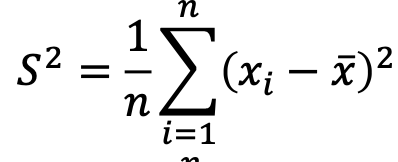

に変えることが出来これを使用し求めることが多いです。
全く必要ないのですが、簡単に何故このようになるか証明します。
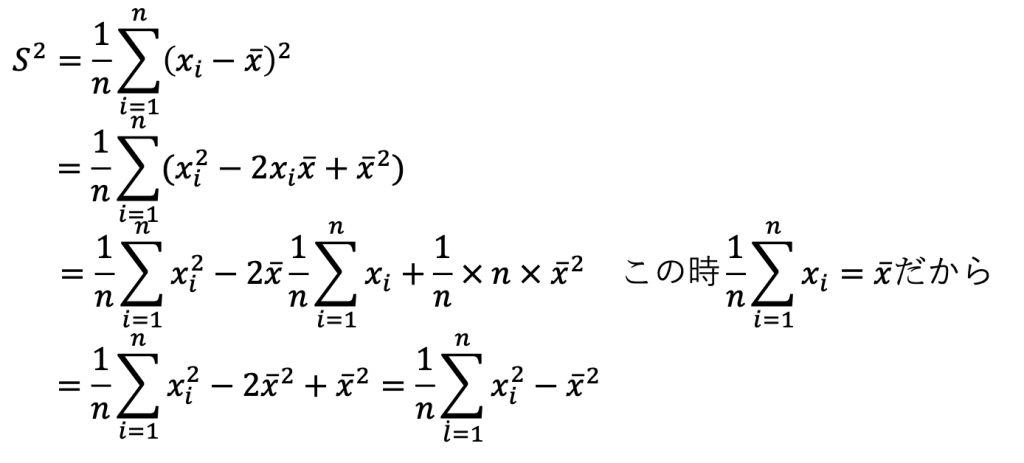
実際の分散の計算
いま、7、9、5、という集合があった場合の分散を電卓で2通りの方法で計算します。
しかし、その前に電卓の使い方を簡単に説明します。
- M+ メモリーに加算(memory plus)
- MR メモリーを呼び出す(memory recall)
- MC メモリーをクリア(memory clear)
- GT =を押したものを加算(grand total)
- CI CE 直前に押した数を訂正
GT及びM+のキーがない電卓は計算が大変難しくなります。
どれだけ大変か、ない場合とある場合の2つの方法で計算する場合を下記に示します。
それでは、実際に計算してみます。
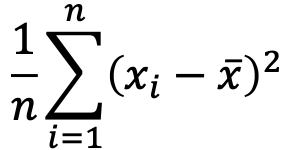
を使って計算する場合
① 最初に平均を計算します。
(7+9+5)÷3=7
電卓では下記の様に計算します。
GTが無い場合 7 、 +、 9、 +、 5、 =
GTがある場合 7 、 =、 9、 =、 5、 =、 GT、 ÷、 3、 =
平均は7と算出されます。
② それぞれのデータから平均を差し引きます。
((7 − 7)2+(9 − 7)2(5 − 7)2))÷3=
電卓では下記の様に計算します。
GTが無い場合 7、-、7、X、=、M+、9、-、7、X、=、M+、5、-、7、X、
=、M+、MR、 ÷、 3、 =
GTがある場合 7をM+で記憶させて 7、-、MR、X、=、9、-、MR、X、=、5、-、MR、X、=、GT、 ÷、 3、 =
今回は平均が7と割り切れた為、M+で記憶させる必要はなかったかもしれませんが、7.3333・・などでしたら入力が大変なのが理解できると思います。
またM+の記憶を消すにはMCを使用します。
分散は2.66・・と算出されます。
試験では下記に示す太字の入力方法がおすすめです。
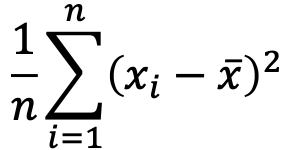
を使って計算する場合
①
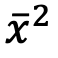
最初に平均の2乗を計算します。
具体的には((7+9+5)÷3)X((7+9+5)÷3)です。
電卓では下記の様に計算します。
GTが無い場合 7 、 +、 9、 +、 5、 =、 ÷、 3、=、 X、=
計算した値49を紙に書きます。
GTがある場合 7 、 =、 9、 =、 5、 =、 GT、 ÷、 3、 = X、=
計算した値をM+で記憶させます。
②

それぞれのデータの2乗をデータ数で除算します。
具体的には((7X7)+(9X9) +(5X5))÷ 3です。
電卓では下記の様に計算します
GTが無い場合 7 、X、= M+、 9、X、=、 M+、 5、 X、=、M+、 MR、 ÷、 3、=
GTがある場合 7 、 X、=、 9、 X、 =、 5、 X、 =、 GT、 ÷、 3、=
③
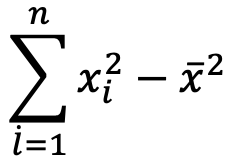
②で求めた値から①で算出した値を引き算します
𝑙ሶ=1
GTが無い場合 2の計算が終わった後、紙に書いた49を引く – 、49 、=
GTがある場合 2の計算が終わった後 -、MR、=
実際に入力すればIIの方が簡単なことが理解できると思います。
平方和の計算
後で出てくるのですが、分散をデータ数で除算しないものを平方和と言います。
データ数を除算していないだけですので平方和も分散と同様に計算すると比較的簡単に算出 されます。
計数値と計量値
もうしばらくすると、計数値 計量値 と言う言葉が出てきます。
このどちらを扱うかで、考え方が大きく変わるため計量値とは とか 計数値とは何かを理解を する必要があります。
具体的な例のでいえば身長は例えば168cmと言いますが 正確には168.12457889・・・・と永遠に 続き数値化できないです。
このようなものを扱う場合 計量値 と言います。
逆に不良数とかを扱う場合 1個の不良とかはあり得ますが、1.5個の不良などはあり得ないです。
このように数えれるものを扱う場合、計数値と言います。
- 数えれるものは 計数値
- 数えれないものは 計量値
と覚えておくとよいと思います。
計量値は連続的で計数値は離散的な扱い。
また計量値の場合168.12457889・・・・という 同じ値が発生することはまずあり得ず、計数値の場合1個の不良は何度も発生することがあります。