12.管理図
はじめに
管理図は異常を見つけるための一手法であり、統計的にあまり起こりえない(0.3%の確率 つまり6σ でしか起こりえないこと)を察知する方法です。
そしてその変動が偶然か異常かを見極めるため、群と群の間で変動しているか、それとも群の中で変動しているのか分けています。
(群:同種のものを 集めたもの)つまり群と群で違いが生じているならば異常原因であり見逃してはいけないもの、逆に 群の中での違いは偶然原因で避けられないものとしているのです。
この手法は最も古く考えられた品質管理手法であり、それがゆえに電卓でさえ、まだ一般的でなく 電卓無しでどのように察知すればよいか様々な手法が出てきます。
管理図の種類
まずは計量値の管理図として表12.1の4つが有名です。

表12.1
Me(中央値)とはデータを大きい順に並べた時の中央の値です。
(例) 例えば 3,8,4,7,9の中央値は大きさ順にならべると3,4,7,8,9となるのでちょうど中央の7が中央値になります。
R(範囲)は最も大きい数値と最も小さい数値の差です。
(例) 例えば 3,8,4,7,9の場合、最大値は9で最小値は3ですので9-3=6が範囲となります。
Rs(移動範囲)は、”今回の値-前回の値の絶定値”です。
(例) 例えば 3,8,4,7,9の場合、|8-3|,|4-8|,|7-4|,|9-7|ですので5,4,3,2となります。
s(標準偏差)は
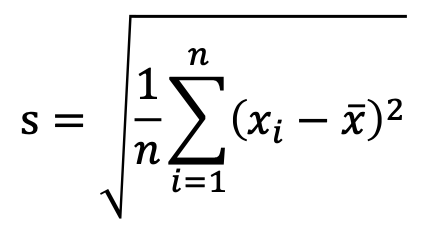
で求められ、
(例) 例えば 3,8,4,7,9の場合 2.588…となります。
次に計数値の管理図として表12.2の4つが有名です。
計数値の場合、下記の2点を留意ください。
調べる対象の大きさで区分
- 調べる対象の大きさが同じ場合は計算をせずにそのままの数を
- 調べる対象の大きさが異なる場合は同じ大きさに計算して数または比率を
調べる対象が複数か1個か違うかで区分
- 複数個:例えば製品n個当たりどれだけ不良品があるかの場合
⇒不良率0はほとんどない⇒二項分布に従う - 1個:例えば製品1個にどれだけ欠点(傷など)があるか
⇒欠点があれば不良品なのでほとんどは0⇒ポアソン分布に従う
まとめると下記のようになります。

表12.2
管理線の求め方
計量値の管理図において 、電卓無しで標準偏差を求めることは困難です。
しかしながら、あらかじめ算出しておいた係数を使用すれば誤差はあるのですが簡単に管理幅や標準偏差が算出されます。
その係数は下記のようになります。
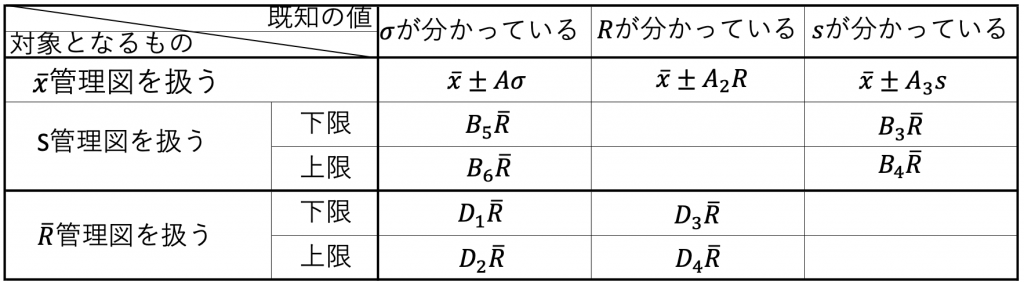
表12.3


計数値の管理図において
