10.検定(補足説明)
はじめに
検定は奥が深く、ある程度手法の勉強が終わったこの第十章で再度検定の勉強をしたいと思います。
第一種の誤りと第二種の誤り
第七章で学習した生産者危険、消費者危険のように検定の間違いも正しい仮説なのに間違っていると考える誤り(第1種の誤り)と、間違っている仮説なのに正しいと考える誤り(第2種の誤り)があり、これが正規分布上ではどのように表されるか第一種の誤りを図10.1で「第二種の誤り」の図10.2で再度説明します。
例として母集団と標本が同じものであるか否かを検定する場合を考えます。
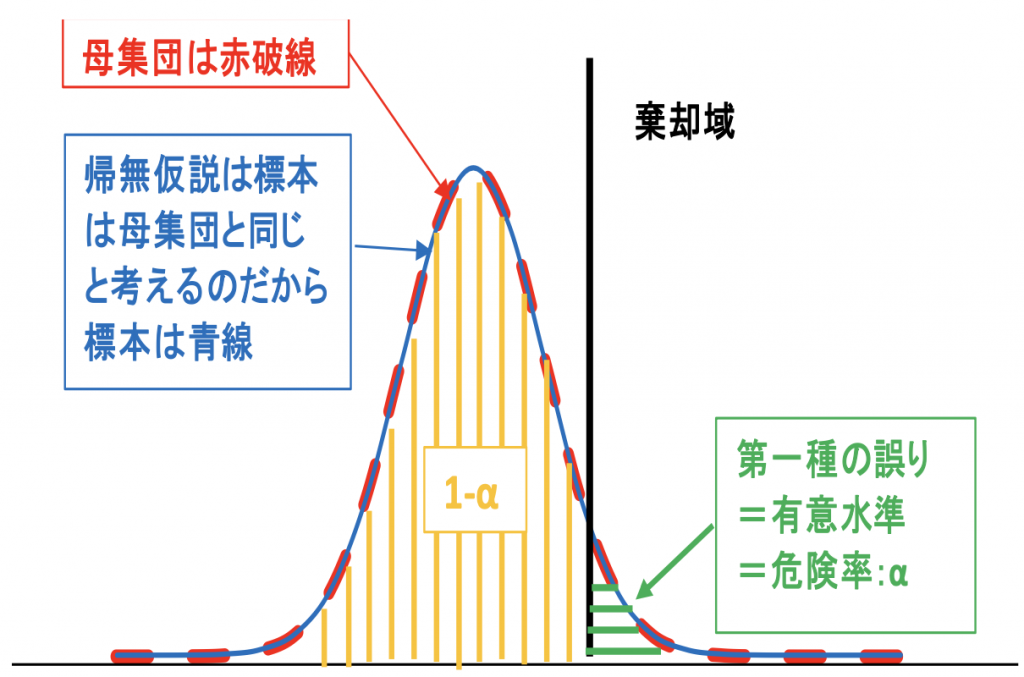
図10.1
まず図10.1の説明ですが、帰無仮説が正しいという事は”標本は母集団と同じ”という事です。
そして、神様ではないのだから間違えても良いと決めた基準が棄却域で黒色で示しています。
そうすると棄却域を挟んで2つの場合が考えられ標本を取った際
- 運悪く緑線の領域を抽出した場合 、本当は母集団と同じにもかかわらず違っていると判断するα
- 当たり前のように黄線の領域を抽出した場合、母集団と同じとは積極的には言えないが帰無仮説が棄却できないと 考える1-α
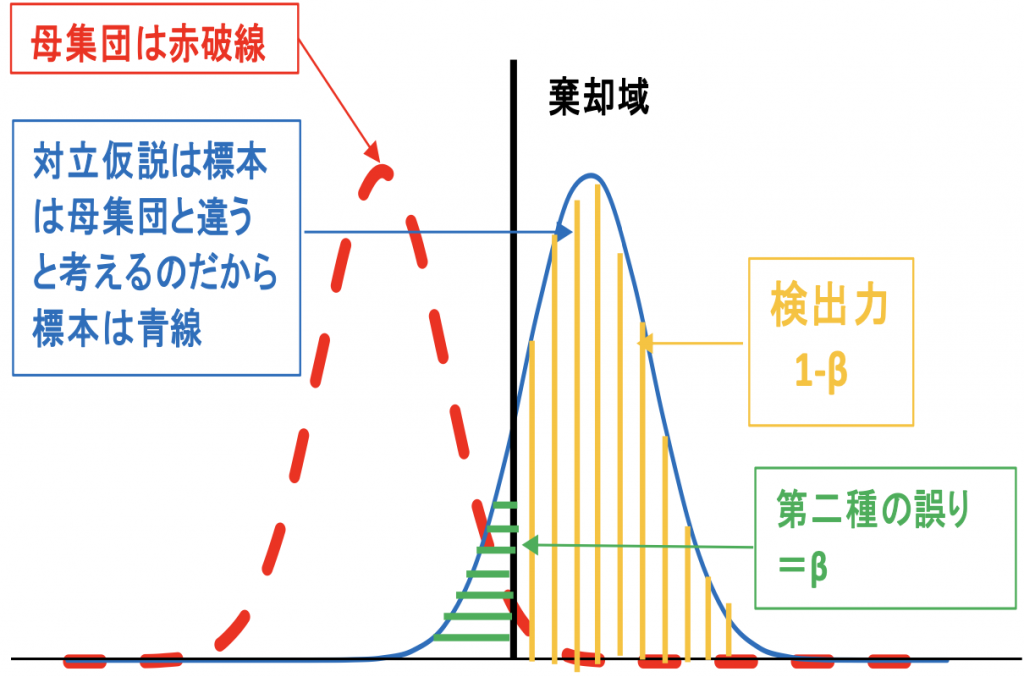
図10.2
次に図10.2の説明ですが、対立仮説 が正しいという事は”標本は母集団と 違う”という事です。
そうすると棄却域を挟んで2つの場合が考えられ
- 運悪く緑線の領域を抽出した場合、本当は母集団と違っているにもかかわらず同じと判断するβ 黄線の領域を抽出した場合、想定通り母集団と異なる領域を抽出したと考える検出力1-β
検出力0.8とは100回仮説検証して80回は標本と母集団は違うと検出出来るという事です。
また図10.2から、棄却域を右に寄せると第一種の誤りが減る代わりに第二種の誤りが増えることが分かると思います。
また、これを表にまとめると表10.1の関係になります。
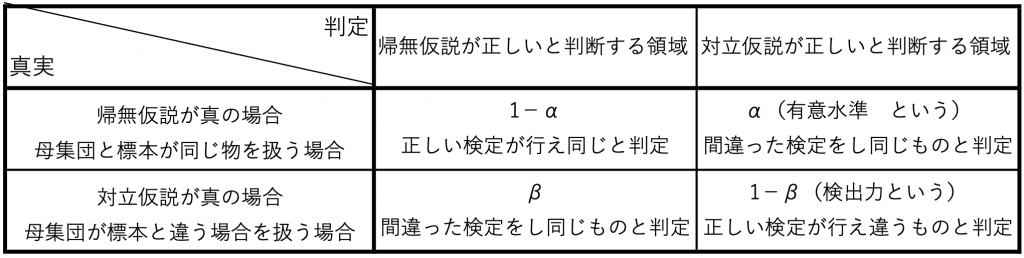
表10.1
相関の検定について
第8章の相関があるか無いかに関しての検定です。
帰無仮説 H0: ρ=0
対立仮説 H1: ρ≠0
として

回帰直線の検定
これも第8章の続きになりますが回帰直線は実はないのだが、誤差によってあるように見えているだけか、それとも本当にあるのかその確認も直線で得られた値と誤差のばらつきを比較することで検定できます。
帰無仮説 a=0
対立仮説 a≠0 傾きが0(無い)という事は相関が無いという事
検定統計量 F0 : VR/VE 規格限界値 F(1,n-2:α) で検定します。
F0を算出するには まず 総平方和や回帰平方和などを計算する事が必要です。
導出の過程も簡単に記載しましたが、過程は覚える必要はなく、結論のみ覚えたらよいのでは無いかと思います。
また実験計画法と同様 『総平方和 = 回帰平方和 + 残差平方和]』に分解し回帰分散と誤差分散を比較し検定するという手段になります。
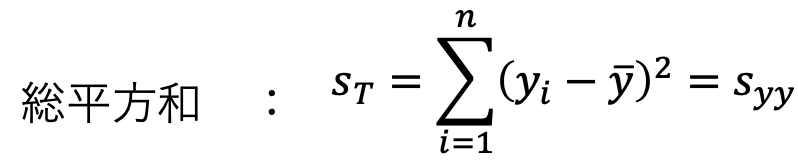

したがって

表10.2
相関と回帰直線の検定の違いに関して
3項、4項で相関に関して別の観点での検定を紹介しました。
この2つの検定の違いは相関は2つの変数xyの関係を見るもの、回帰関係は変数xで変数yをどれだけ説明できるかということです。
実験計画法の検定に関して
分散分析は、3章で説明した検定と異なり複数の集団を同時に検定できます。
3章の検定方法だと、例えば母集団A、母集団B、母集団Cを有意水準5%で検定する場合どうしても母集団Aと母集団B、母集団Aと母集団C、母集団Bと母集団Cを検定する必要があります。
結果、1つの検定をするのに有意水準5%の検定を3回行うということです。
これは5%の間違える可能性が3回生じる。
つまり1 − 0.953 = 0.14つまり14%も間違える可能性が高くなるのです。
この観点からも分散分析はとても有用です。
独立性のχ2検定(かいにじょうけんてい)
独立性の検定を説明して、この単元を終えたいと思います。
独立性とは例えば、A工場B工場C工場の不良の出方において工場間による違いがないか (=関係がない=独立しているか)のような検定です。
具体的には同じ製品をA工場、B工場、C工場で製造しており、その結果が表10.3のようになったとします。
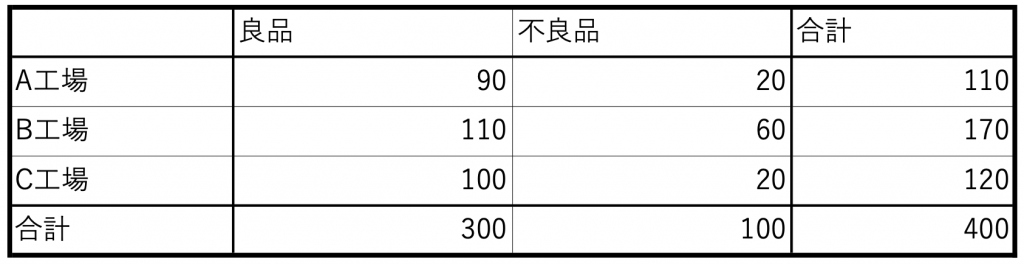
表10.3 データ表
この場合、工場によって良品と不良品の出方に違いがあるかどうか検定しなさいというような問題です。
回答としては、
①
A工場とB工場C工場にもし関係がないとするならば良品と不良品の数はどうなるか考えます。
- A工場 B工場 C工場を合わせた製造の良品数は300
不良品数は100なので、工場間に関係ない良品:不良品の割合は3:1です(3/4は良品 1/4は不良品) - 工場間で不良発生の確率に変化がないとするならばA工場は110個製品を製造しているので良品数は90÷4X3=67.5個 のはずです。
- 2のようにすべてを工場間に変化がないとした場合の計算を行うと表10.4の分割表ができます。

表10.4
②
表10.4で工場間で不良発生比率が変わらない場合の値を計算したが、当然その値は現実の値表とは異なります。
そこで、ここでは現実の値と違いがないと考えた場合の値にどれだけ違いがあるかを計算します。
計算手順は
- 現実の値から違いがないと考えた場合の値を引き算します
- 1の引き算だけでは計算値がプラスやマイナスになります。
しかし、違いの大きさが知りたいのだから符号は必要なく2乗し符号をなくします。
(現実の値 − 期待している値)²(10.1) - 私たちは現実の値が理想の値(期待値)とどの程度の隔たりがあるか
知りたいのだから(10.1)式を理想の値で除算して割合にします。
⇒理想との値との比較にする。

割合にする理由ですが、もし割合にしないと例えば今回はデータ数が400個ですが、データ数が1000や2000になると(データ数が増えただけで)(10.1)式ですと隔たりが少なくても隔たりが大きいとなるからです。
そして、少し余談になり、しかも正確とは言えないのですが、実は(10.2)式が χ2分布の横軸を示し、縦軸は横軸の確率(正確には確率密度)になるのです。
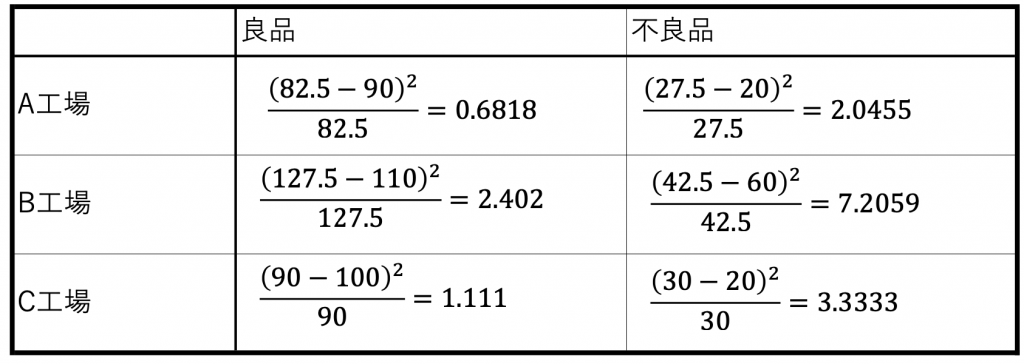
表10.5
4. この各要素の値を合計します。 0.6818+2.0455+2.402+7.2059+1.1111+3.3333=16.7995
χ2検定統計量と比較します。
この時、自由度は表の(行数-1)X(列数-1)になるのだから
(3-1)X(2-1)=2X1=2
また 有位水準5%の場合
値は χ2=16.795>χ2(2,0.05)=5.99 が成立し、有意水準5%で有意になります。