4.検定
はじめに
第3章 推定の応用が検定で、これを利用すると、理論的構築がなくても魔法のように2つの母集団を比較し、この母集団が違うものかどうかなどが判定ができます。
例えば男女の間には身長の違いはあると思います。
この事実は経験的に知っているだけで確たる説明はできません。
しかし男女の身長を測定することでこれを数学的に男女間には身長差があると判定できるのです。
そして、これを検定といいます。
検定の考え方
前項の推定の勉強で、標本を取りだし計算することで、例えば集団Aの母平均は95%の確率で

の間にあると分かりました。
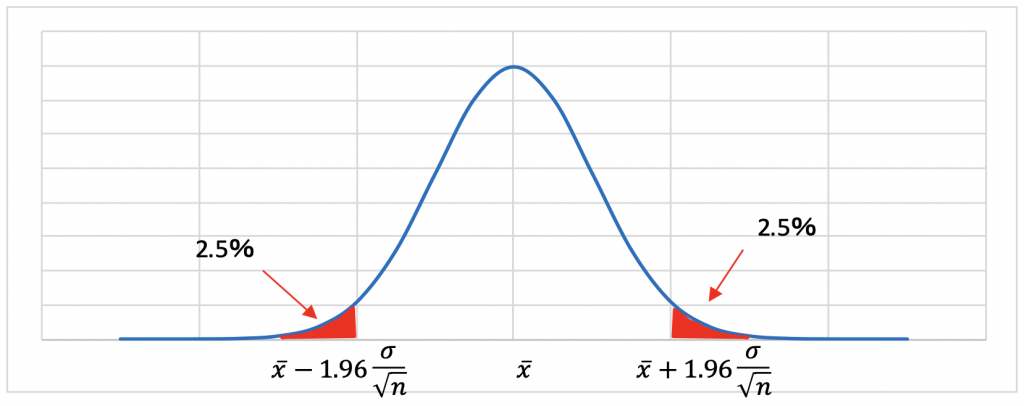
図示すると図4.1のようになります。
次に、3.13式の範囲に入らない(赤塗部に)母平均を持つ集団Bがあったとします。
(具体的には母集団Aは成人男性の身長 母集団Bは成人女性の身長 などを想定したら考えやすい かもしれません)
この場合考え方が2つで
- 母集団Aと母集団Bは95%の確率で別の集団である。
- 5%しか起こりえないまれなことが発生したが母集団Aと母集団Bは同じものである。
があります。
そして、検定では検定をする前に何%の間違いを許容するか先に定めます。
(許容範囲の多くは95%ないし99%)そして推定された範囲内にあるか(この値を検定統計量 という)を確認し、無ければ95%の確率で同じ母集団であるとはいえないと結論づけます。
ここで注意するのが、理論的に推論されたものではないので同じ母集団 であるとかは断定はできないのです。
否定しか出来ないのです。
控え目に95%の確率で同じ母集団ではないと考えれるというだけです。
しかし、逆に考えれば理論的に推論しなくても、同じ母集団とは考えれないという数値データだけで判断を下せるという素晴らしいツールでもあるのです。
検定統計量
検定で大切なのは検定統計量でこの値が図4.1の赤塗り部にあるかどうかで判断します。
繰り返しになりますが図の分布は3.12式より
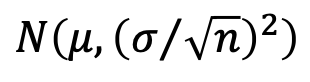
です。
この分布を直接使用し95%の区間を算出するには

(既出1.6) を計算する必要があるので、すでに計算され表になったものがある標準正規分布に変換します。
つまり
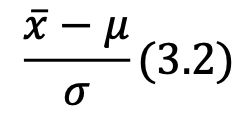
を使い
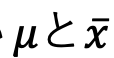
は母平均の分布のためそのまま
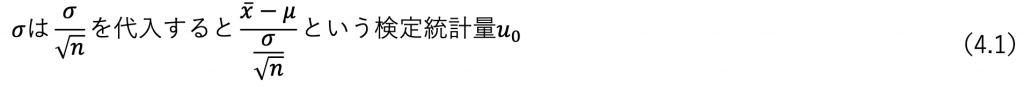
が算出され、これを用いて判定を下すのです。
(母分散既知つまり母標準偏差も既知の場合)
検定の用語
検定は先の推定と数学的には同じ考え方なので数式に多くの変化はありません。
しかしながら、 独特の思考を行うため、多くの用語が発生しそれについて書きます。
統計的に検定するということは、論理的証拠が無いのだからこれは正しいと積極的に肯定すること は不可能で例えば95%の確率で同じ母集団ではないと否定するのみとなります。
このことから、
- 主張したい説の反対を先に言って、それが否定されたのだから反対の説が正しいのではないかとの手順を踏みます。
主張したい説の反対つまり無にしたい、無に帰したい説を帰無仮説。
その逆の主張したい説を対立仮説といいます。
通常、帰無仮説はH0、対立仮説はH1で示されます。
(Hは仮説を意味するhypothesisの頭文字) (ここで0は基準となるものの意味で使用。後述となるがμ0も同様) - そして、無事帰無仮説が否定されることを帰無仮説が棄却され対立仮説が採択された、もしくは有意差があるという歯切れの悪い言い回しをします。
断定できないので仕方ないのですが・・
逆に帰無仮説が否定されない場合、帰無仮説が受容されたとか有意差がないと表現します。 - ところでこの95%という値は、検定を行おうとする人が検定を始める前に100-95=5%の確率を外れて起きる事柄ならばその仮説は意味があると定めた水準でありこの値を有意水準といいます。
もちろん検定前に検定する人が決める水準ですので95%にこだわる必要はなく99%でもよいです。
また、逆に考えれば5%の確率で正しい仮説を間違っていると判断する可能性があるため危険率とも言います。 - 図1の赤塗りの箇所に検定統計量が入ればその仮説は棄却されるのでこの赤塗り個所を 棄却域 といいます。
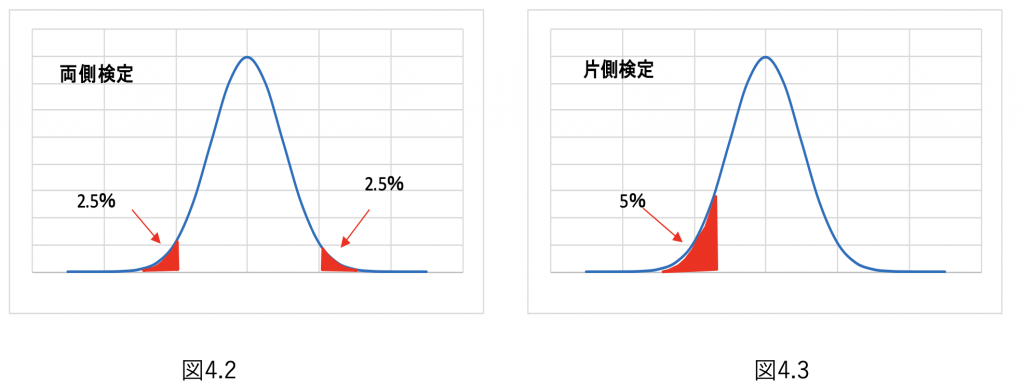
そして逆の範囲は採択域といいます。 - 母集団に変化があったかのように推定値が下がることもあれば上がることもあるような検定を行う場合、図4.2の 両側検定を使用します。
逆に改善を行った結果不良率が下がったかなどの場合は推定値が下がったのみを検定すればよいので図4.3の片側検定を使用します。
この時、気付いてほしいのが両側検定よりも片側検定のほうが同じ95%の有意水準でも棄却域 が大きくなり対立仮説が採択されやすくなる ということです。
実際の検定
例に挙げた男女間の身長差の検定は今は難しいため、今回は最も簡単な検定の仕方を説明します。
10年前に大規模に日本人成人男性の身長を測定したところ平均身長170cm 標準偏差が5cmであった。
今回、食生活の影響などで平均身長が変化したのではないかと考え偏りなく100名の身長を測定したところ平均は172cmであった。
身長が10年前と比較し高くなっているか検定しなさい。
但し、標準偏差は変わらなかったと考える このような問いがあったとします。
解答としては、
1 仮説をたてる
帰無仮説H0として 標本平均μは母平均 μ0と同じである 対立仮設H1として 標本平均μは母平均μ0と異なる これを数式で表すと
H0:μ0=μ
H1:μ0≠μ
となります。
ここで注意してほしいのは母平均が標本平均(100名の身長平均)と変化したかの問いの場合身長が高くても低くても変化しているので両側検定のμ≠μ0を使用します。
もし問いが身長が高くなっているかの問いの場合は片側検定のμ0<μを使用します。
説明の簡易化のため 今回は大きくなっているかで検定します。
すなわち
H0:μ0=μ
H1:μ0<μ となります。
2 有意水準の設定
これ以下の確率で物事が生じているならば帰無仮説を棄却しようという境界線の値です。
通常は有意水準αは0.05(95%)か0.01(99%)に設定することが多いので今回は0.05で設定します。
これを数式で表すとα=0.05
3 棄却域の設定
α=0.05と設定したのだから正規分布表よりP=0.05を読み取りとなります。
難しいのでμ0<μ の片側検定にしたのですが、両側検定の場合、両側に棄却域があるため𝑢 0.025 = 1.96を使用します。
今回は片側なので𝑢 0.05 =1.645
4 検定統計量の計算
検定統計量の公式に当てはめて統計検定量を計算します。
今回の場合は

棄却域を表す記号は𝒖で検定統計量を表す記号は𝒖𝟎ということを留意してください。
参考までに、
標本数が10人の場合 検定統計量u0=1.26 となります。
標本数が少ないと判定が困難になるということでしょう。
この検定統計量4がとる確率をP値といい今回の場合読み取ると0.00003になります。
これは10年前と今の平均身長が変化していないという可能性が0.0003%の確率であるということになります。
P値を定義すると 帰無仮説が正しい場合に、起こりうる最大の確率となります。
5 判定
この時、対立仮説でどのような仮定したかが大切になります。
頭がこんがらかるので、最初のうちは下記のような図4.4を記載し検定統計量と棄却域 の関係を理解するようにした方が良いです。
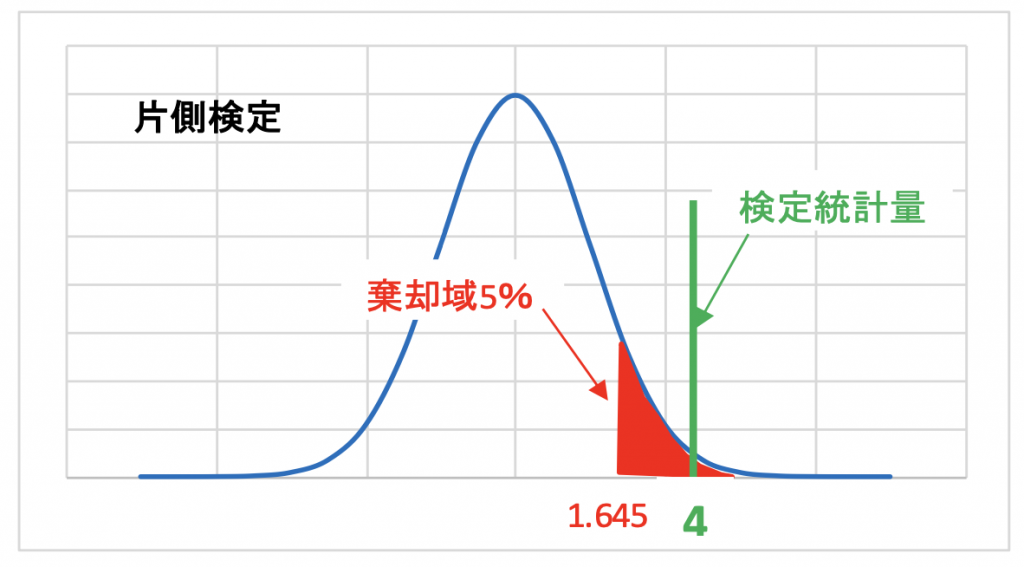
結果、検定統計量の4は棄却域(帰無仮説が正しくないと判断する領域)に入っているので
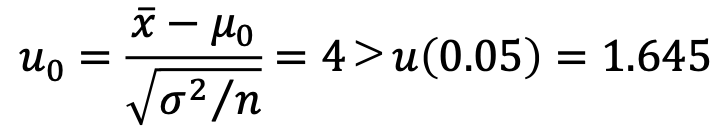
の関係が成立し、帰無仮説は棄却され身長は高くなった と判定されるのです。
(くどいようですが 式の不等号の向きは 図4.4 を理解して判定してください)
補足説明
第3章においても5項において補足説明をしたのですが、第4章においても補足説明が必要です。
ひとつは、今回1例を挙げただけですが、実はデータに対応がある場合の検定や平均ではなく分散がどうかなど多くの検定があります。
本稿の目的は考え方の理解ですのでその内容は記載しません。
しかしもう一つ。
第8章などを勉強した後説明したほうが良い検定の種類があります。
これは別途、第10章で説明します。