1.工程能力とは
はじめに
今、私たちは50±0.5mmの長さの品物を作らないといけないとします。
この時 条件1と条件2で 出来たものを測定した結果が以下のようになったとします。
条件1
49.4 50.4 50.0 50.2 49.8 50.2 50.6 50.0 50.4 49.6 49.8 50.0 49.6 49.8 50.2 50.0
条件2
50.2 50.0 49.4 49.8 50.2 50.2 49.8 49.6 50.0 49.8 50.2 49.8 49.6 50.0 49.6 50.2
この時、どちらの条件で作ったほうが不良が出にくいでしょうか?
多分、データが多すぎて判断 が難しいと思います。
そのため、条件1で作ったときのデータの集団 条件2で作ったときのデータ の集団それぞれを一つの数値で表せれば判断が簡単です。
あるデータの集団を1つの数値に表わしたものを代表値といい代表値の中には
- 最大値 ・・・数値の集団の中で最も大きな値
- 最頻値 ・・・数値の集団の中で最もよく出た値
- 平均値 ・・・数値の集団を平らに均(なら)して得られる値
等があり、平均は算数のテストの平均点は 等のように日常的にもっともよく使用される値です。
平均とは
条件1の平均を求め方は
(49.4+50.4+50.0+・・・・・+50.2+50.0)÷16 のように全てのデータを加味して(加えて)、しかし、全てのデータを加えるだけだとデータ数 が多いほど値が大きくなるので、その値をデータ数で割って求めます。
これを式で表すと
49.4 をx1 50.4をx2 50.0をx3 ・・・・・50.2をx15 50.0をx16と仮に定め (x1+x2+x3+・・・+x15+x16)÷16 となり公式が非常に長くなるので、Σ(シグマ 全部を寄せ集めるという意味)という記号を用いてもっと簡単に書きます。

参考までに、下記は、𝑖が1から𝑛までの𝑥𝑖 について全てを寄せ集める(足し算を行う)と言う意味です。
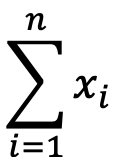
標準偏差とは
平均を計算しますと条件1は50.0 条件2は49.9となります。
また規格の中心値は50.0ですのでこの 値は条件1の平均と同じであり条件1の方がよい条件のような気がします。
しかし本当にそうでしょうか?
条件1の場合49.4~50.6までの数値があり規格外れが2つ。
それに対して条件2の場合は49.4~50.2までで規格外れは1つのみです。
条件1と2ではどちらのデータのバラつきが小さいかを考慮する必要があります。
バラつきをみるのにはどうしたらよいでしょうか?
バラつきを見るのには何か基準を作り、その基準に対してどれだけ違いがあるか考えたらよさそうです。
せっかく2項で平均を求めたのですから、それを基準にしてどれだけ離れているか各々の数値の引き算を行います。
50.0-49.4=0.6 50.0-50.4=-0.4 50.0-50.0=0 ・・50.0-50.2=-0.2 50.0-50.0=0
しかし、上の数値はマイナスやプラスがありますが私たちはどれだけバラついているか知りたいのであって、マイナスやプラスは邪魔です。
そこで マイナス×マイナス=プラスの公式を利用 して上の数値を全て二乗します。
(0.6)² (-0.4)² (0)² ・・・・ (-0.2)² (0)²
そうすると 条件1の場合
0.36 0.16 0 0.04 0.04 004 0.36 0 0.16 0.16 0.04 0 0.16 0.04 0.04 0 のようなデータの集団ができます。
はじめに にあったように上の数値の集団ではデータが多すぎるため、平均を使って一つにまとめます。
そうすると
- 条件1の場合 (0.36+0.16+0+・・・+0.04+0) ÷16=0.1
- 条件2の場合 (0.09+0.01+0.25+・・・+0.09+0.09) ÷16=0.065
つまり、条件2の方が条件1よりもバラつきが小さいとわかります。
実は今まで求めてきた値を分散と言い数値のバラつきを示すのによく用いられ

で示すことができます。
また、分散は全ての数値を二乗しているので、この値を平方根したもの(単位を平均と同じにしたもの)を標準偏差と言い 次式で表すことができます。

ところで今求めた値は実験数(データ数)nで割っているのですが、多くの場合はn-1(自由度) で割ることが多いです。
理由は条件1の実験数(データ数)16で求めた分散は0.1ですが実験数 (データ数)を100、200と増やした場合の分散は0.1ではなく(0.36+0.16+・・+0.04+0) ÷(16-1)=0.1066に近いと数学的に証明されているからです。
数学的証明は難しくて割愛致しますが、データのうちの1つは基準として使用されるためデータ数として認めていない。
またデータ数が大きくなればなるほど1を引いた影響は小さくなるからと考えてください。
n-1で割って得た分散や標準偏差は不偏分散 不偏標準偏差と言われます。 (不偏 つまり かたよりがない という意味)
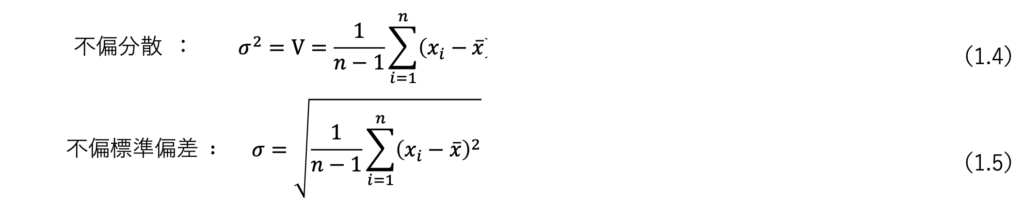
正規分布とは
平均では条件1が、バラツキでは条件2が良いとなり、どちらの条件が良いか分からなくなってきました。
平均とバラツキ 両方を考慮した指針が必要です。
この指針が工程能力ですが、それを求める前に、少し趣向を変えて条件1で得たデータの棒グラフを作成してみます。
まずどの数値が何回出ているか個数を求めると以下のような表ができます。
| データ | 49.4 | 49.6 | 49.8 | 50 | 50.2 | 50.4 | 50.6 |
| 個数 | 1 | 2 | 3 | 4 | 3 | 2 | 1 |
これを棒グラフにすると図1.1のようになります。
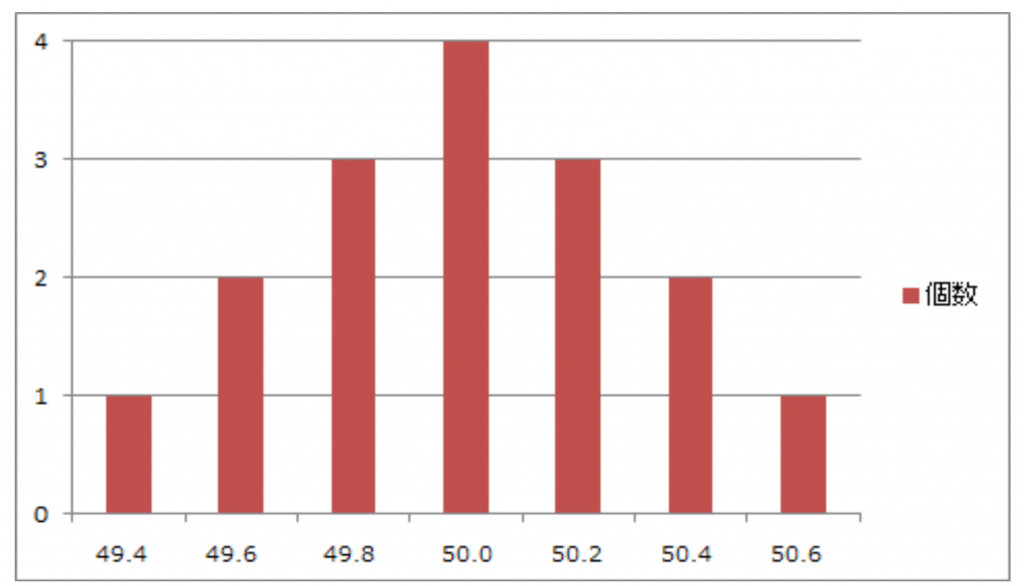
実は同じ条件下で出来たものを棒グラフで表すと、データ数が多くなればなるほど平均値のものが多く発生し平均値から離れれば離れるほど段々少なくなる、つまり図1のような釣鐘状のような形になる(これを正規分布と言います)と言われています。
参考までに同じ条件下でない場合、つまり18才の男性と18才の女性の身長を一緒にして棒グラフを作った場合、男性の平均と女性の平均の二つのこぶがあるような分布になります。
工程能力とは
さて 急に難しくなりますが、この棒グラフの形は次式で示すことができます。

具体的には図1.2のようになります。
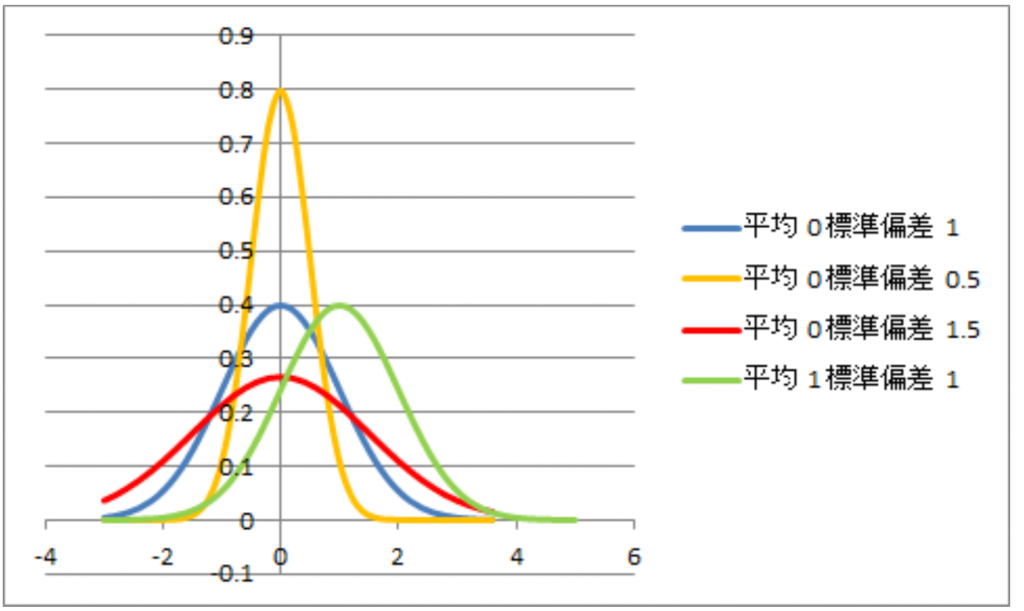
先程、求めた平均Xがグラフの最も高いところを標準偏差σがバラつきを示す事が分かると思います。
ところで何故式で示す必要があるのでしょうか?
式で示すことが可能になれば、式を積分するなど色々加工することによって発生する割合等が算出でき便利だからです。
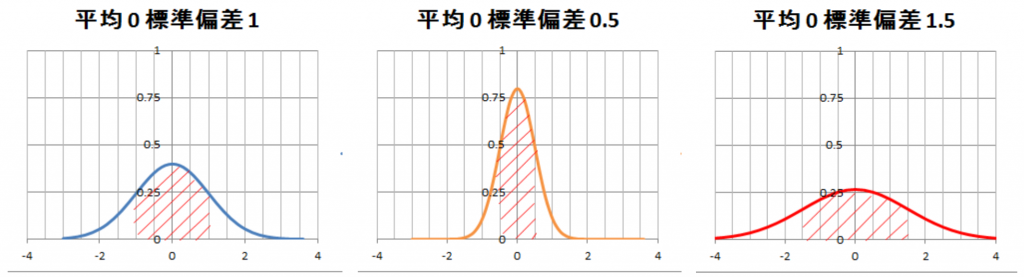
また、もう一つの特徴として 分布の中心線(平均)から標準偏差 までの面積は、平均や標準偏差の値が変化しても常に一定であることが図3からも感覚的に分かると思います。
つまり標準偏差が意味することは、平均±標準偏差の範囲に全データの68.3% (図1.3の赤斜線部分の面積)が入るとなります。
ここで特に平均から3σないし4σ離れて物事が生じることはまれである。
まれに生じるかどうか 判断しようというのが工程能力の基本的な考えです。
つまり上限規格と下限規格の範囲が3σに入っているかどうか見比べる(割り算を行う)ということです。
(標準偏差の単位は規格値と同じなので(今回の場合ならmmなので)規格値と同系列に 見比べることが可能)具体的には工程能力Cpは

(但しデータの平均値と規格の中央値が同じ場合) で示されます。
このことを表で見ますと図1.4のようになります。
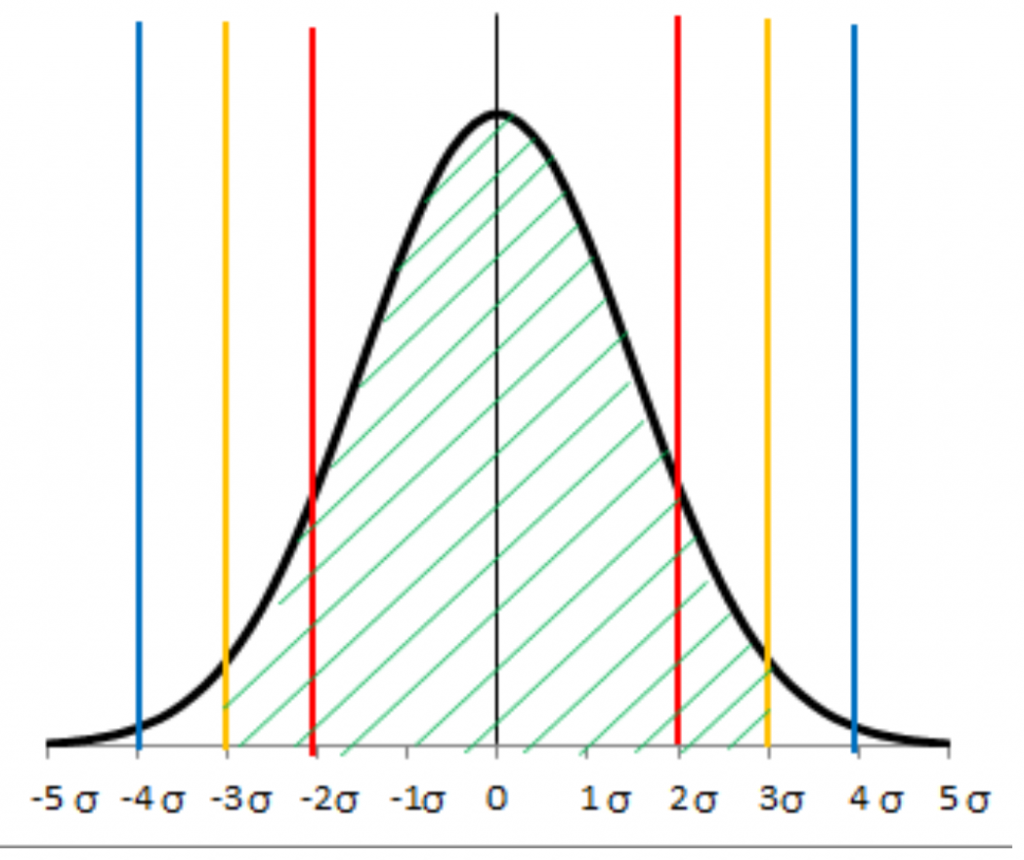
- 上限規格 下限規格が3σより小さい場合(赤) 値は1以下
- 上限規格 下限規格が3σと等しい場合(黄) 値は1
- 上限規格 下限規格が3σより大きい場合(青) 値は1以上
特に上限規格と下限規格が4σと一致する場合、値は4÷3=1.333 となり、この値より大きいと工程能力は十分と言われています。
ところで実際は図4のようにデータの平均と規格の中央値が一致することはまれです。
そのため補正する必要がありますが、その前に大きければ大きいほど良いなど規格が片方しかない場合は下記のようになります。

そして、データの平均と規格の中央値の値が異なった場合、工程能力は下記の式で算出されます。

ここで、𝑚𝑖𝑛(𝑐𝑝𝑈,𝑐𝑝𝐿)は𝑐𝑝𝑈と𝑐𝑝𝐿の小さいほうの値を意味します。
結果
- 条件1の工程能力Cpは0.510 Cpkも0.510
- 条件2の工程能力Cpは0.633 Cpkは0.506
となりますが、どちらにしても1.333には程遠いです。
もっと条件か規格を見直さなければ量産は難しいということになります。